Difference between revisions of "Elliptic E"
From specialfunctionswiki
| Line 15: | Line 15: | ||
=References= | =References= | ||
[http://web.mst.edu/~lmhall/SPFNS/spfns.pdf "Special Functions" by Leon Hall] | [http://web.mst.edu/~lmhall/SPFNS/spfns.pdf "Special Functions" by Leon Hall] | ||
| + | |||
| + | [[Category:SpecialFunction]] | ||
Revision as of 18:37, 24 May 2016
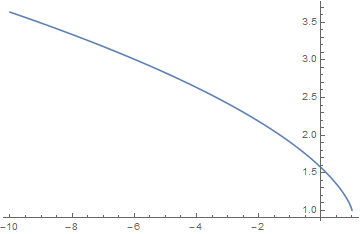
If $m=k^2$ we define the complete elliptic integral of the second kind, $E$, to be $$E(k)=E(m)=\displaystyle\int_0^{\frac{\pi}{2}} \sqrt{1-k^2\sin^2 \theta} d\theta.$$
- Domaincoloringelliptice.png
Domain coloring of $E(m)$.
See Also
Elliptic K
Incomplete Elliptic E