Difference between revisions of "Elliptic K"
From specialfunctionswiki
| Line 1: | Line 1: | ||
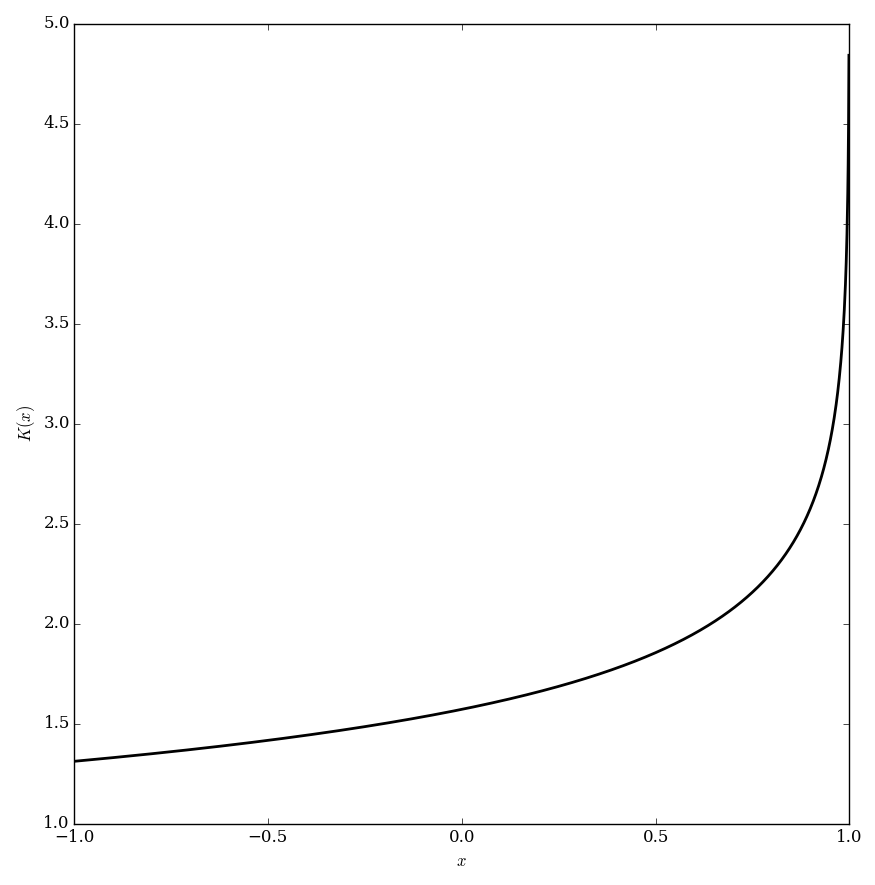
The Elliptic $K$ function is also known as the complete Elliptic integral of the first kind. If $m=k^2$ we define the complete elliptic integral of the first kind, $K$ to be | The Elliptic $K$ function is also known as the complete Elliptic integral of the first kind. If $m=k^2$ we define the complete elliptic integral of the first kind, $K$ to be | ||
| − | $$K(k)=K(m)=\displaystyle\int_0^{\frac{\pi}{2}} \dfrac{1}{\sqrt{1-k^2\sin^2 \theta}} d\theta.$$ | + | $$K(k)=K(m)=\displaystyle\int_0^{\frac{\pi}{2}} \dfrac{1}{\sqrt{1-k^2\sin^2 \theta}} \mathrm{d}\theta.$$ |
<div align="center"> | <div align="center"> | ||
Revision as of 17:00, 25 May 2016
The Elliptic $K$ function is also known as the complete Elliptic integral of the first kind. If $m=k^2$ we define the complete elliptic integral of the first kind, $K$ to be $$K(k)=K(m)=\displaystyle\int_0^{\frac{\pi}{2}} \dfrac{1}{\sqrt{1-k^2\sin^2 \theta}} \mathrm{d}\theta.$$
Graph of $K$.
Domain coloring of $K$.
See Also
Elliptic E
Incomplete Elliptic K
