Difference between revisions of "Ceiling"
From specialfunctionswiki
| Line 1: | Line 1: | ||
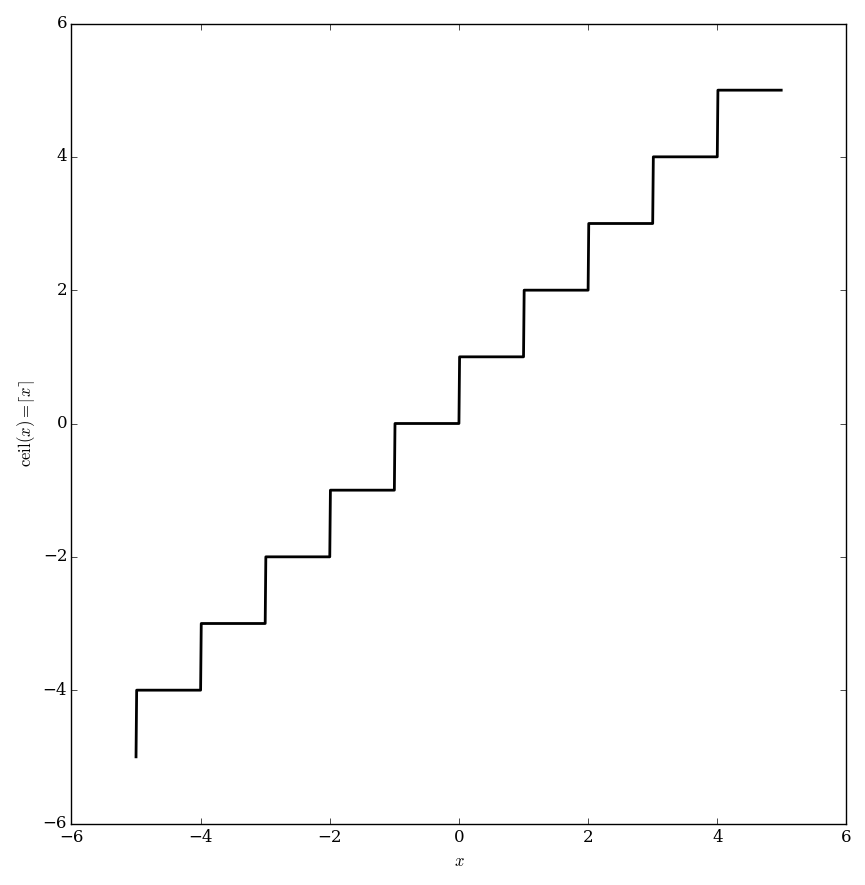
| − | The ceiling function $\ | + | The ceiling function $\mathrm{ceil} \colon \mathbb{R} \rightarrow \mathbb{Z}$ is defined by |
| − | $$\ | + | $$\mathrm{ceil}(x) = \min \{ y \in \mathbb{Z} \colon y \geq x \},$$ |
| − | i.e., the smallest integer greater than or equal to $x$. | + | i.e., the smallest integer greater than or equal to $x$. It is sometimes denoted by $\lceil x \rceil$. |
<div align="center"> | <div align="center"> | ||
Revision as of 19:48, 3 June 2016
The ceiling function $\mathrm{ceil} \colon \mathbb{R} \rightarrow \mathbb{Z}$ is defined by $$\mathrm{ceil}(x) = \min \{ y \in \mathbb{Z} \colon y \geq x \},$$ i.e., the smallest integer greater than or equal to $x$. It is sometimes denoted by $\lceil x \rceil$.
Graph of $\mathrm{ceil}$.
