Difference between revisions of "Spherical Hankel h (1)"
From specialfunctionswiki
| Line 8: | Line 8: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =See Also= | ||
| + | [[Spherical Bessel j]] <br /> | ||
| + | [[Spherical Bessel y]]<br /> | ||
<center>{{:Hankel functions footer}}</center> | <center>{{:Hankel functions footer}}</center> | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 21:11, 3 June 2016
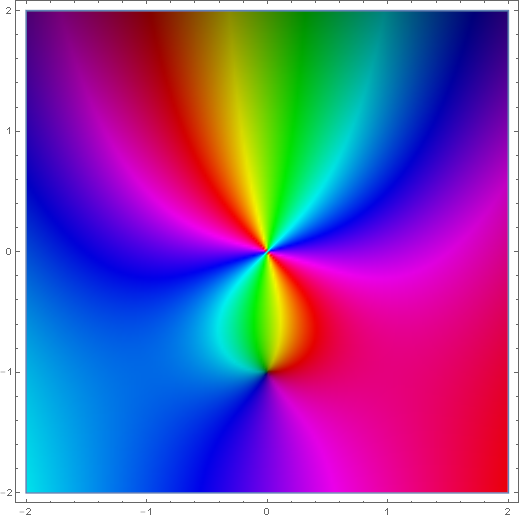
The spherical Hankel function $h_{\nu}^{(1)}$ is defined by $$h_{\nu}^{(1)}(z)=j_{\nu}(z)+iy_{\nu}(z),$$ where $j_{\nu}$ is the spherical Bessel function of the first kind and $y_{\nu}$ is the spherical Bessel function of the second kind.
Domain coloring of analytic continuation of $h_1^{(1)}(z)$.
See Also
Spherical Bessel j
Spherical Bessel y
Spherical Hankel $h_{\nu}^{(1)}$
