Difference between revisions of "Logarithm"
| Line 1: | Line 1: | ||
The (single-valued) logarithm $\log \colon \mathbb{C} \setminus (-\infty,0] \rightarrow \mathbb{C}$ defined by the formula | The (single-valued) logarithm $\log \colon \mathbb{C} \setminus (-\infty,0] \rightarrow \mathbb{C}$ defined by the formula | ||
$$\log(z) = \displaystyle\int_1^z \dfrac{1}{t} dt,$$ | $$\log(z) = \displaystyle\int_1^z \dfrac{1}{t} dt,$$ | ||
| − | where we understand the integral $\displaystyle\int_1^z$ as a contour integral over a | + | where we understand the integral $\displaystyle\int_1^z$ as a contour integral over a path from $1$ to $z$ that does not intersect the set $(-\infty,0] \subset \mathbb{C}$. |
The logarithm restricted to $(0,\infty)$ is the [[inverse function]] of the [[exponential function]]. | The logarithm restricted to $(0,\infty)$ is the [[inverse function]] of the [[exponential function]]. | ||
Revision as of 05:17, 4 June 2016
The (single-valued) logarithm $\log \colon \mathbb{C} \setminus (-\infty,0] \rightarrow \mathbb{C}$ defined by the formula $$\log(z) = \displaystyle\int_1^z \dfrac{1}{t} dt,$$ where we understand the integral $\displaystyle\int_1^z$ as a contour integral over a path from $1$ to $z$ that does not intersect the set $(-\infty,0] \subset \mathbb{C}$. The logarithm restricted to $(0,\infty)$ is the inverse function of the exponential function.
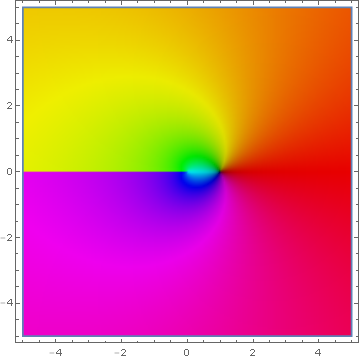
Domain coloring of analytic continuation of $\log$ with branch $(-\infty,0)$.
Contents
Properties
Taylor series of $\log(1-z)$
Taylor series of $\log(1+z)$
Proposition: $\displaystyle\int \log(z) dz = z \log(z)-z$
Proof: █
Theorem: For $|z|<1$, $$\log(1+z) = -\displaystyle\sum_{k=1}^{\infty} \dfrac{(-1)^k z^k}{k}.$$
Proof: █
Relation to other special functions
Theorem
The following formula holds: $$\log(1+z)=z{}_2F_1(1,1;2;-z),$$ where $\log$ denotes the logarithm and ${}_2F_1$ denotes the hypergeometric pFq.
Proof
Calculate $$\begin{array}{ll} z{}_2F_1(1,1;2;-z) &= z\displaystyle\sum_{k=0}^{\infty} \dfrac{1^{\overline{k}}1^{\overline{k}}}{2^{\overline{k}}k!} (-z)^k \\ &= \displaystyle\sum_{k=0}^{\infty} \dfrac{\left( \frac{\Gamma(k+1)}{\Gamma(1)} \right)^2}{\left( \frac{\Gamma(2+k)}{\Gamma(2)} \right)k!}(-1)^k z^{k+1} \\ &= \displaystyle\sum_{k=0}^{\infty} \dfrac{(k!)^2(-1)^k}{(k+1)!k!} z^{k+1} \\ &= \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{k+1} z^{k+1} \\ &= -\displaystyle\sum_{k=1}^{\infty} \dfrac{(-1)^k z^k}{k} \\ &= \log(1+z), \end{array}$$ by the Taylor series of $\log(1+z)$. █
References
Theorem
The following formula holds for $x>0$: $$\mathrm{Ei}(x) = \gamma + \log x + \displaystyle\sum_{k=1}^{\infty} \dfrac{x^k}{kk!},$$ where $\mathrm{Ei}$ denotes the exponential integral Ei, $\log$ denotes the logarithm, and $\gamma$ denotes the Euler-Mascheroni constant.
Proof
References
- James Whitbread Lee Glaisher: On certain definite integrals involving the exponential-integral (1881)... (previous)... (next) (note: expresses the logarithm term as $\frac{1}{4}\log(x^4)$)
Theorem
The following formula holds: $$P(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\mu(k)}{k} \log \zeta(kz),$$ where $P$ denotes the Prime zeta function, $\mu$ denotes the Möbius function, $\log$ denotes the logarithm, and $\zeta$ denotes the Riemann zeta function.