Difference between revisions of "Modified Bessel I"
From specialfunctionswiki
| Line 13: | Line 13: | ||
[[Relationship between Bessel I sub -1/2 and cosh]]<br /> | [[Relationship between Bessel I sub -1/2 and cosh]]<br /> | ||
[[Relationship between Bessel I sub 1/2 and sinh]]<br /> | [[Relationship between Bessel I sub 1/2 and sinh]]<br /> | ||
| + | [[Relationship between Bessel I sub n and Bessel J sub n]]<br /> | ||
| + | [[Relationship between Airy Bi and modified Bessel I]]<br /> | ||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
<strong>Proposition:</strong> The following formula holds: | <strong>Proposition:</strong> The following formula holds: | ||
| Line 22: | Line 24: | ||
</div> | </div> | ||
| − | |||
| − | |||
<center>{{:Bessel functions footer}}</center> | <center>{{:Bessel functions footer}}</center> | ||
Revision as of 08:05, 5 June 2016
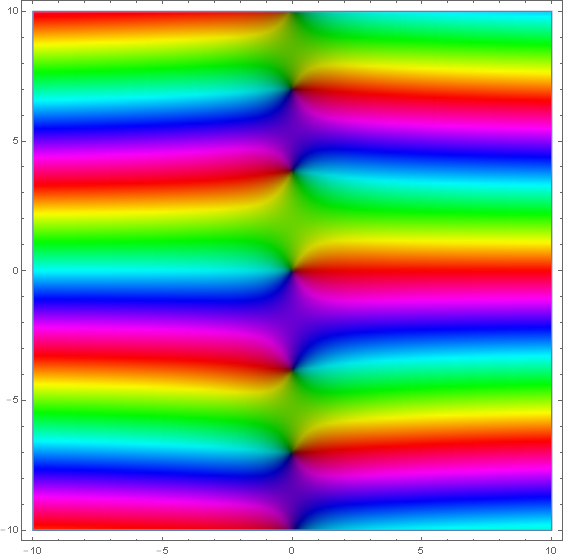
The modified Bessel function of the first kind is defined by $$I_{\nu}(z)=i^{-\nu}J_{\nu}(iz),$$ where $J_{\nu}$ is the Bessel function of the first kind.
Domain coloring of analytic continuation of $I_1(z)$.
Modified Bessel functions from Abramowitz&Stegun.
.jpg)
Properties
Relationship between Bessel I sub -1/2 and cosh
Relationship between Bessel I sub 1/2 and sinh
Relationship between Bessel I sub n and Bessel J sub n
Relationship between Airy Bi and modified Bessel I
Proposition: The following formula holds: $$I_{\nu}(z)=\displaystyle\sum_{k=0}^{\infty} J_{\nu+k}(z) \dfrac{z^k}{k!},$$ where $J_{\nu}$ denotes the Bessel function of the first kind.
Proof: █
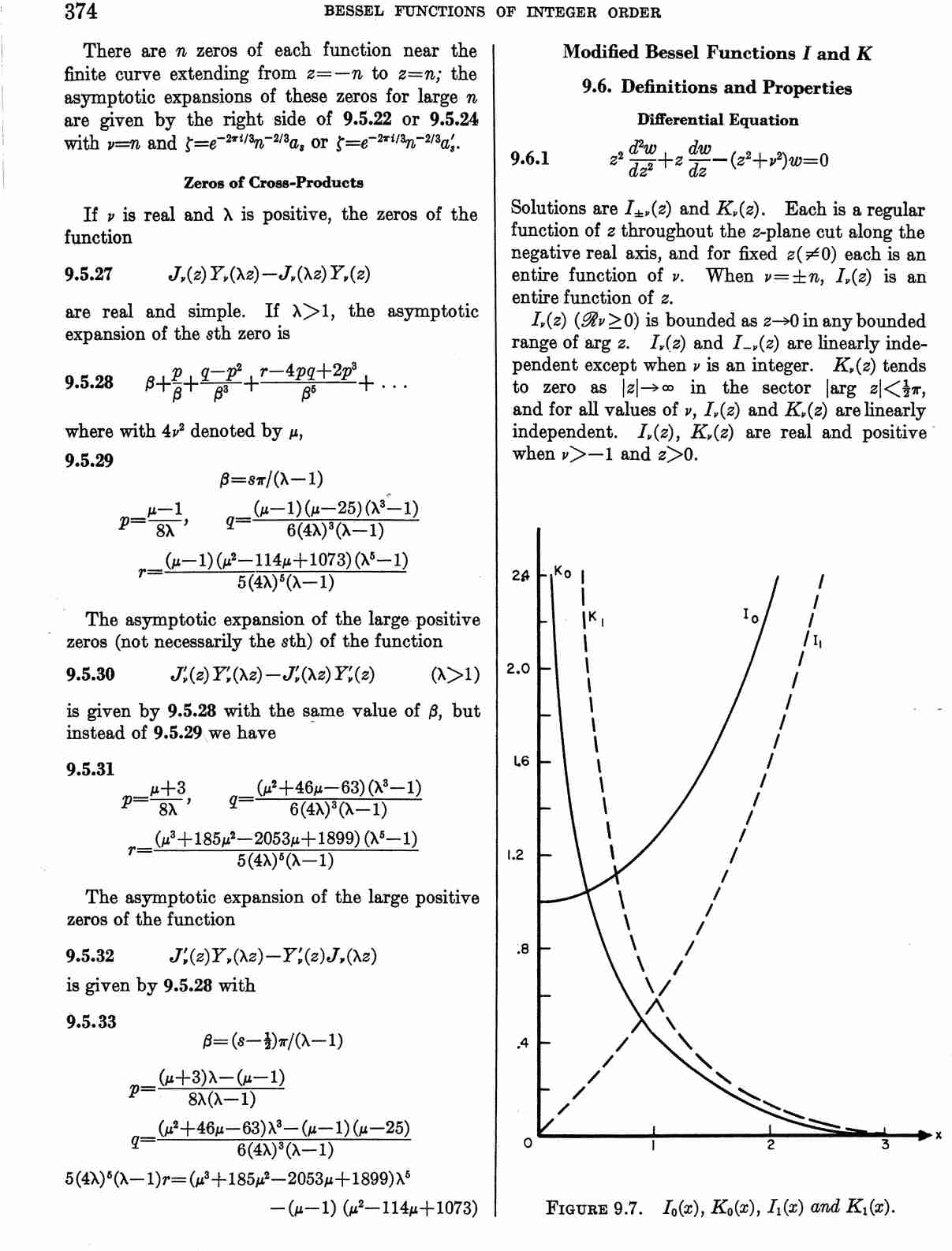
Bessel $I_{\nu}$
