Difference between revisions of "Anger function"
From specialfunctionswiki
| Line 29: | Line 29: | ||
=References= | =References= | ||
| − | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Relationship between modified Struve L and modified spherical Bessel j functions|next=Anger of integer order is Bessel J}}:12.3.1 | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Relationship between modified Struve L and modified spherical Bessel j functions|next=Anger of integer order is Bessel J}}: 12.3.1 |
Latest revision as of 04:05, 6 June 2016
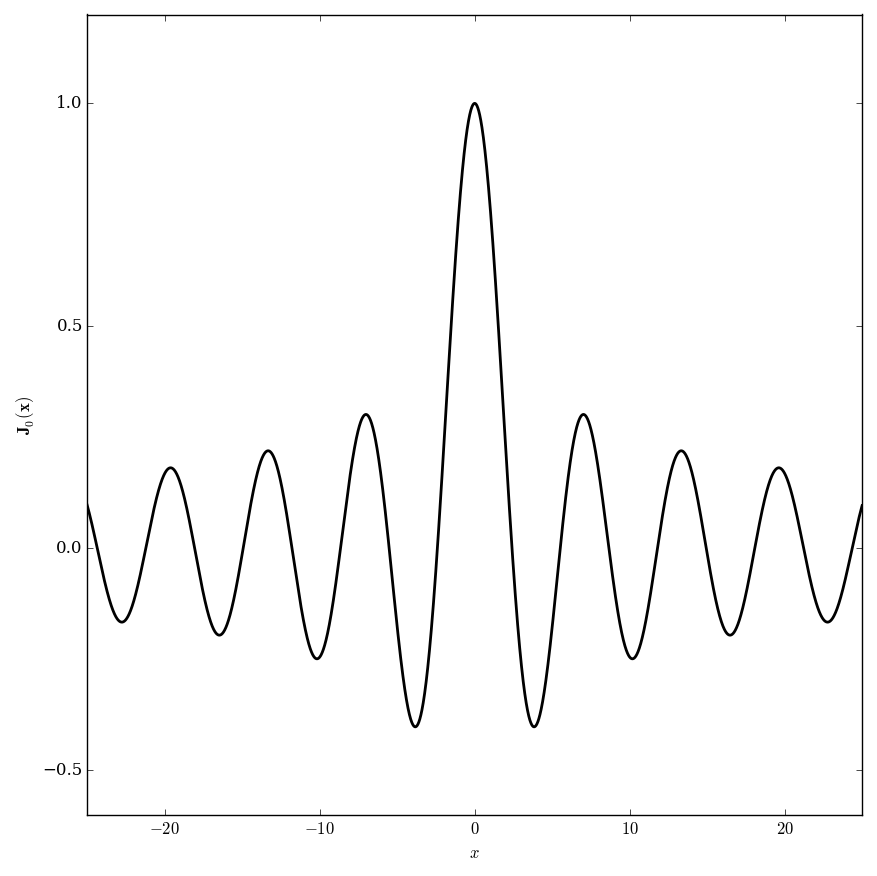
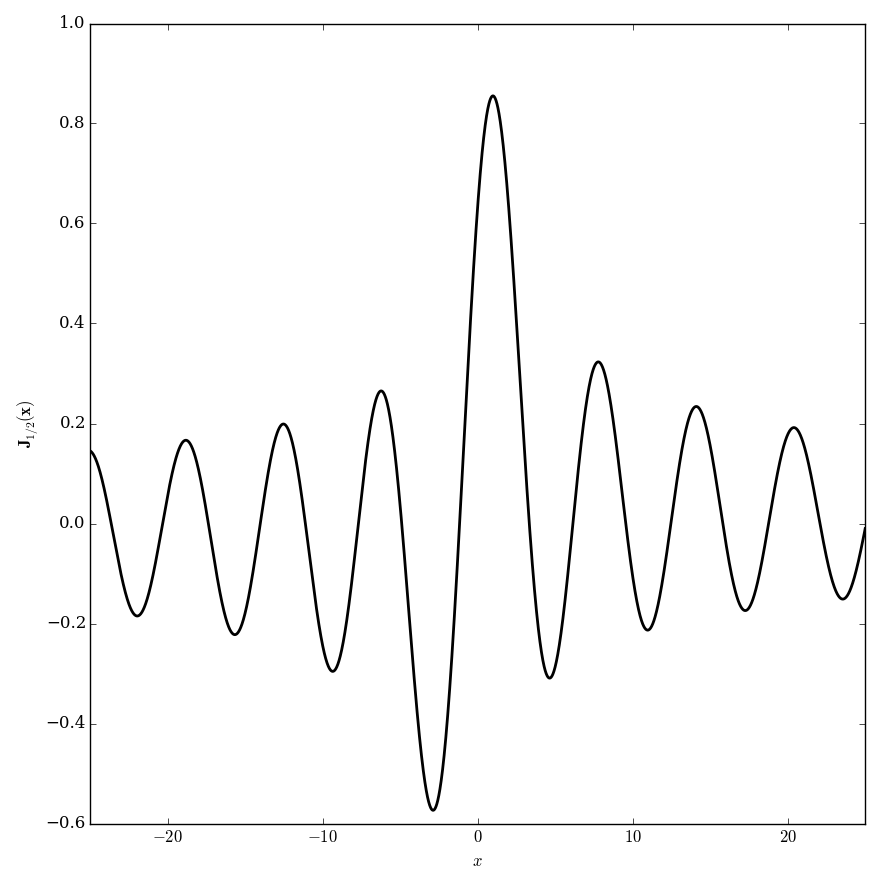
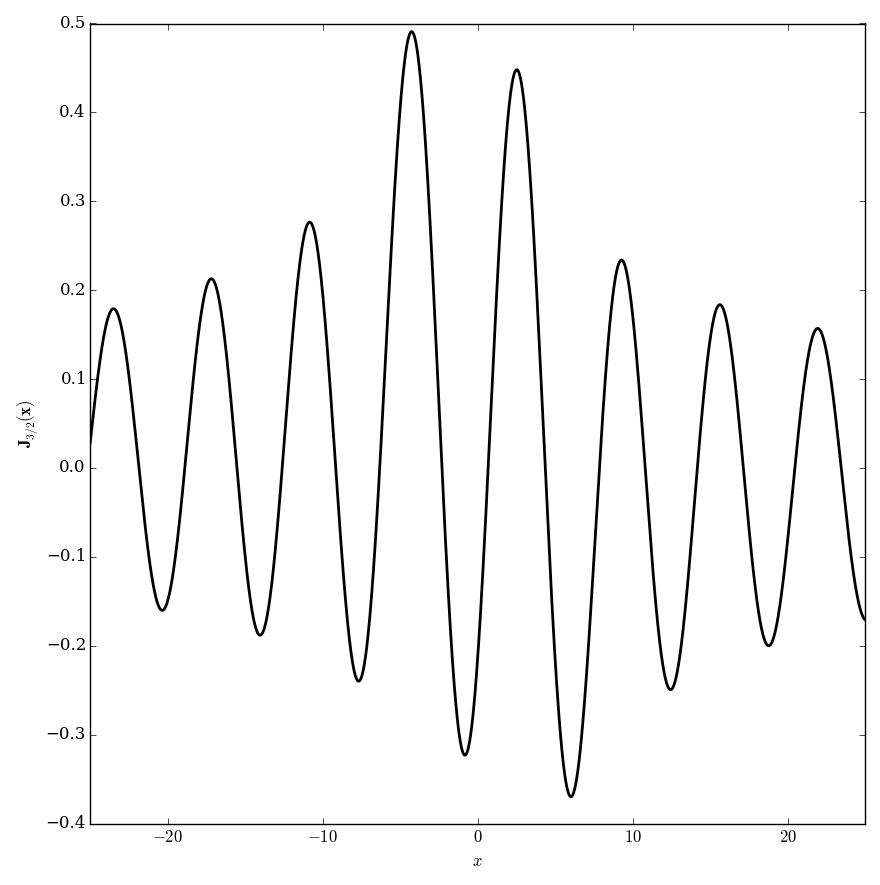
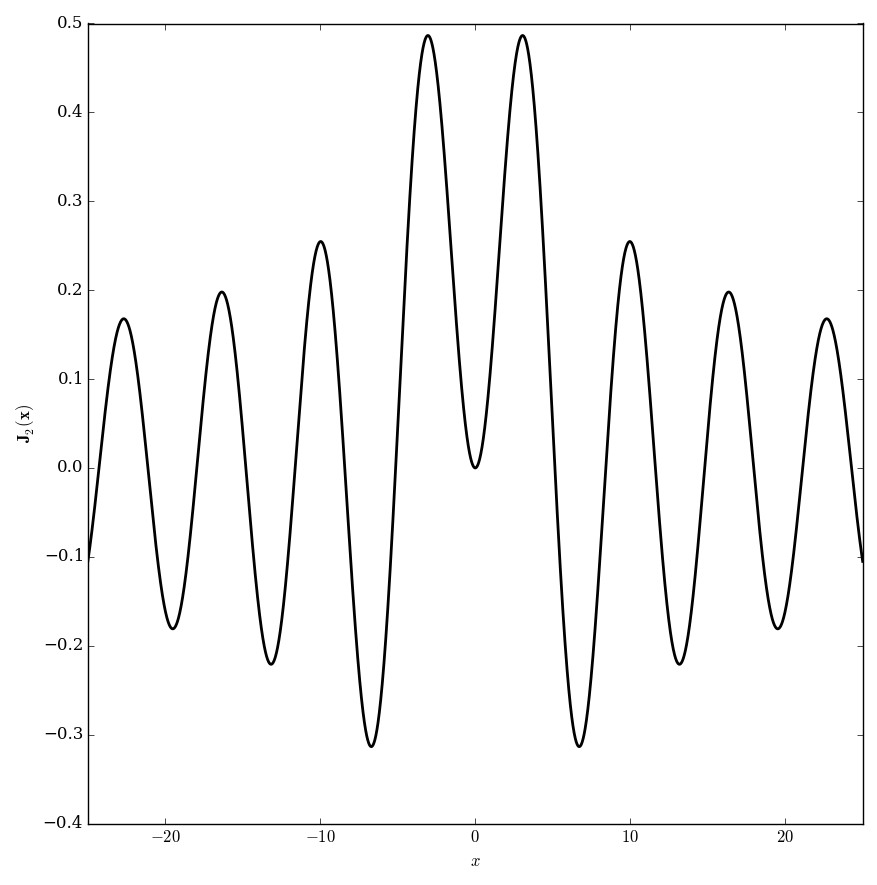
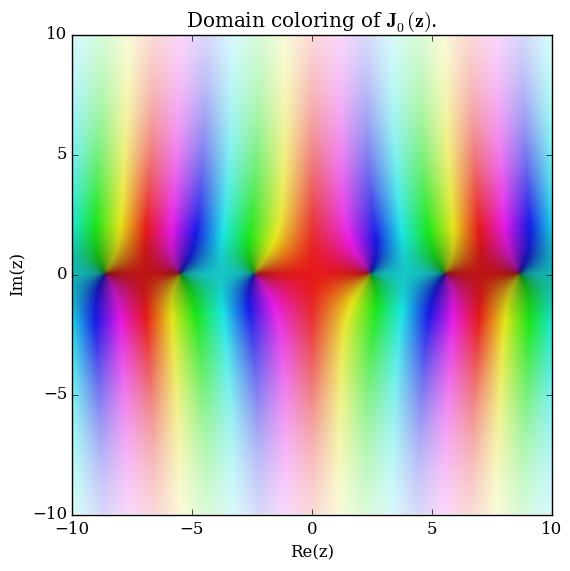
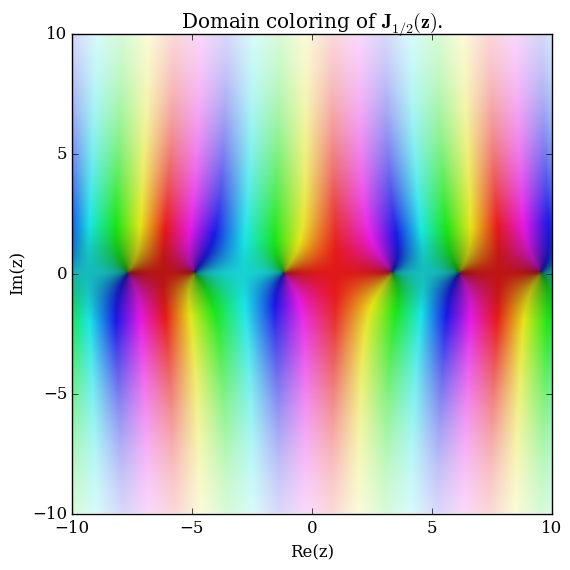
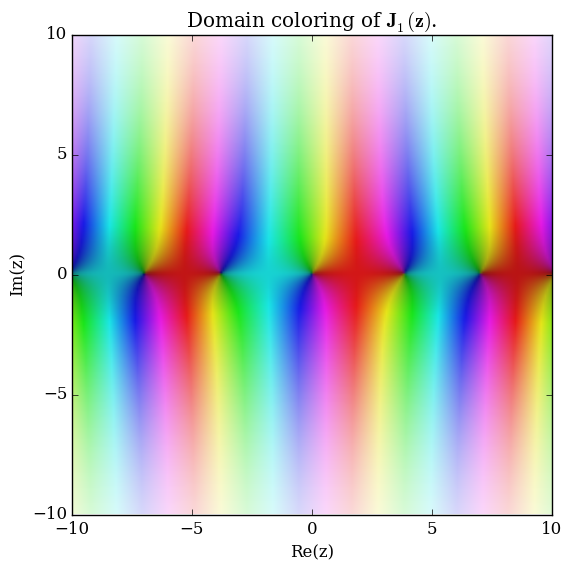
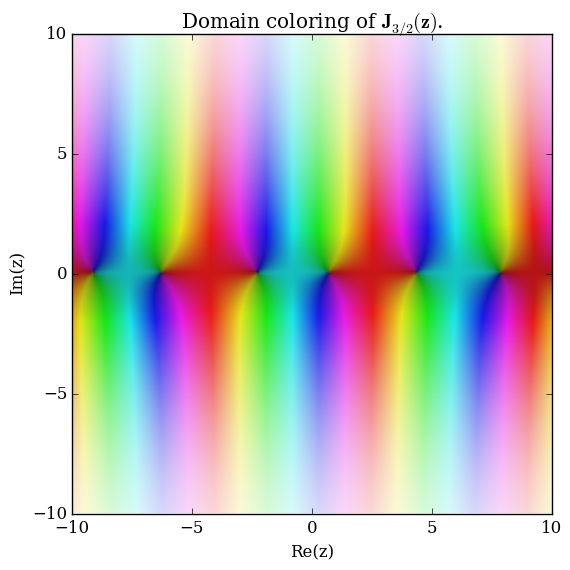
Let $\nu \in \mathbb{C}$. The Anger function $\mathbf{J}_{\nu}$ is defined by $$\mathbf{J}_{\nu}(z) = \dfrac{1}{\pi} \displaystyle\int_0^{\pi} \cos(\nu \theta - z \sin(\theta)) \mathrm{d}\theta.$$
Graph of $\mathbf{J}_0$.
Graph of $\mathbf{J}_{\frac{1}{2}}$.
Graph of $\mathbf{J}_{\frac{3}{2}}$.
Graph of $\mathbf{J}_2$.
Domain coloring of $\mathbf{J}_0$.
Domain coloring of $\mathbf{J}_{\frac{1}{2}}$.
Domain coloring of $\mathbf{J}_1$.
Domain coloring of $\mathbf{J}_{\frac{3}{2}}$.
Properties
Value of Anger at 0
Anger recurrence relation
Anger derivative recurrence
Relationship between Anger function and Bessel J sub nu
Relationship between Weber function and Anger function
Relationship between Anger function and Weber function
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 12.3.1
