Difference between revisions of "Exponential"
From specialfunctionswiki
| Line 16: | Line 16: | ||
[[Euler E generating function]]<br /> | [[Euler E generating function]]<br /> | ||
[[Continued fraction for 1/sqrt(pi) integral from -infinity to infinity of e^(-t^2)/(z-t) dt]]<br /> | [[Continued fraction for 1/sqrt(pi) integral from -infinity to infinity of e^(-t^2)/(z-t) dt]]<br /> | ||
| + | |||
| + | ==References== | ||
| + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Logarithm (multivalued) of the exponential}}: 3.3.1 | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
[[Category:Definition]] | [[Category:Definition]] | ||
Revision as of 20:44, 6 June 2016
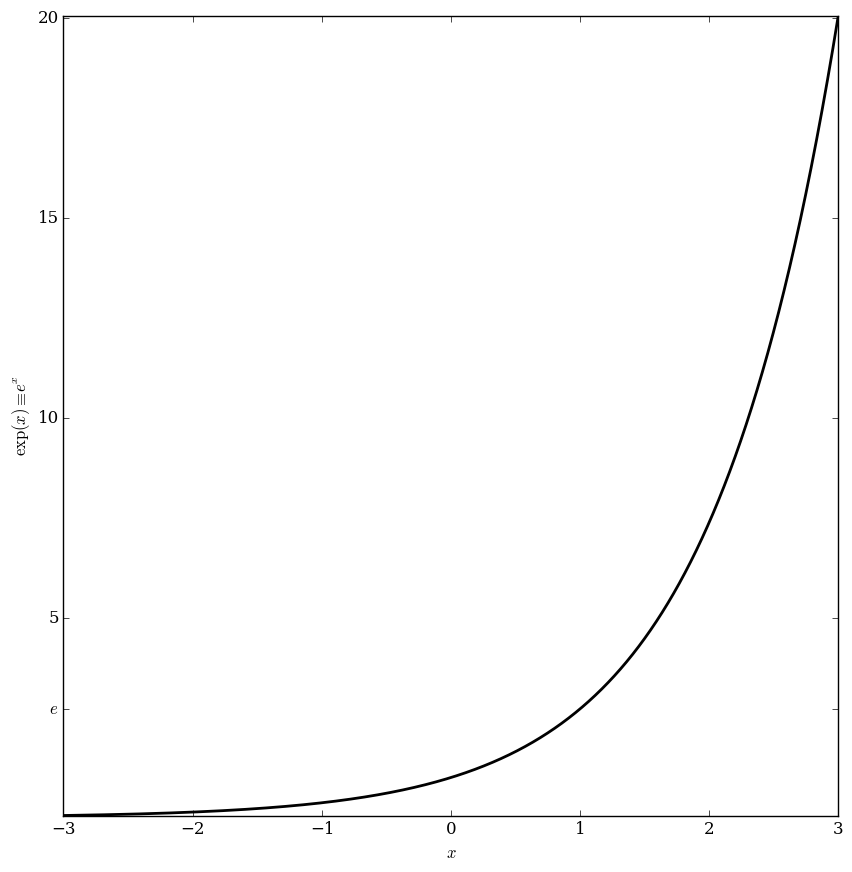
The exponential function $\exp \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula $$\exp(z) = e^z = \sum_{k=0}^{\infty} \dfrac{z^k}{k!},$$ where $e$ is the base of the natural logarithm.
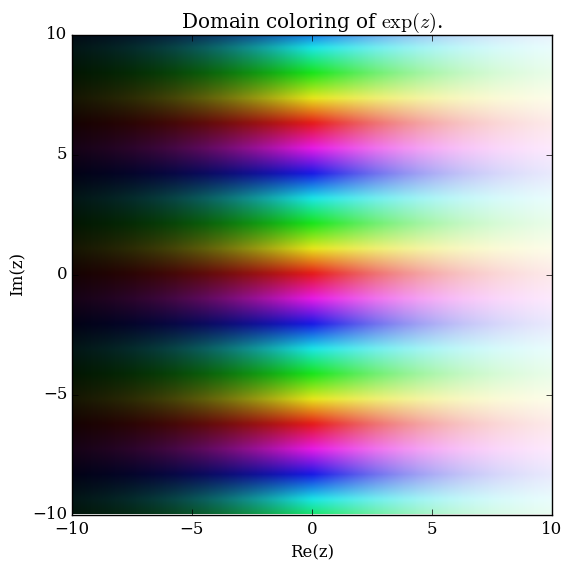
Domain coloring of $\exp$.
Properties
Derivative of the exponential function
Taylor series of the exponential function
Exponential in terms of hypergeometric 0F0
Euler E generating function
Continued fraction for 1/sqrt(pi) integral from -infinity to infinity of e^(-t^2)/(z-t) dt
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 3.3.1