Difference between revisions of "Arcsinh"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| − | The inverse hyperbolic sine function $\mathrm{arcsinh} \colon \mathbb{R} \rightarrow \mathbb{R}$ function is the [[inverse function]] of the [[sinh|hyperbolic sine]] function | + | __NOTOC__ |
| − | + | The inverse hyperbolic sine function $\mathrm{arcsinh} \colon \mathbb{R} \rightarrow \mathbb{R}$ function is the [[inverse function]] of the [[sinh|hyperbolic sine]] function. | |
| − | |||
| − | |||
<div align="center"> | <div align="center"> | ||
| Line 12: | Line 10: | ||
=Properties= | =Properties= | ||
| − | + | [[Derivative of arcsinh]]<br /> | |
=See Also= | =See Also= | ||
Revision as of 07:57, 8 June 2016
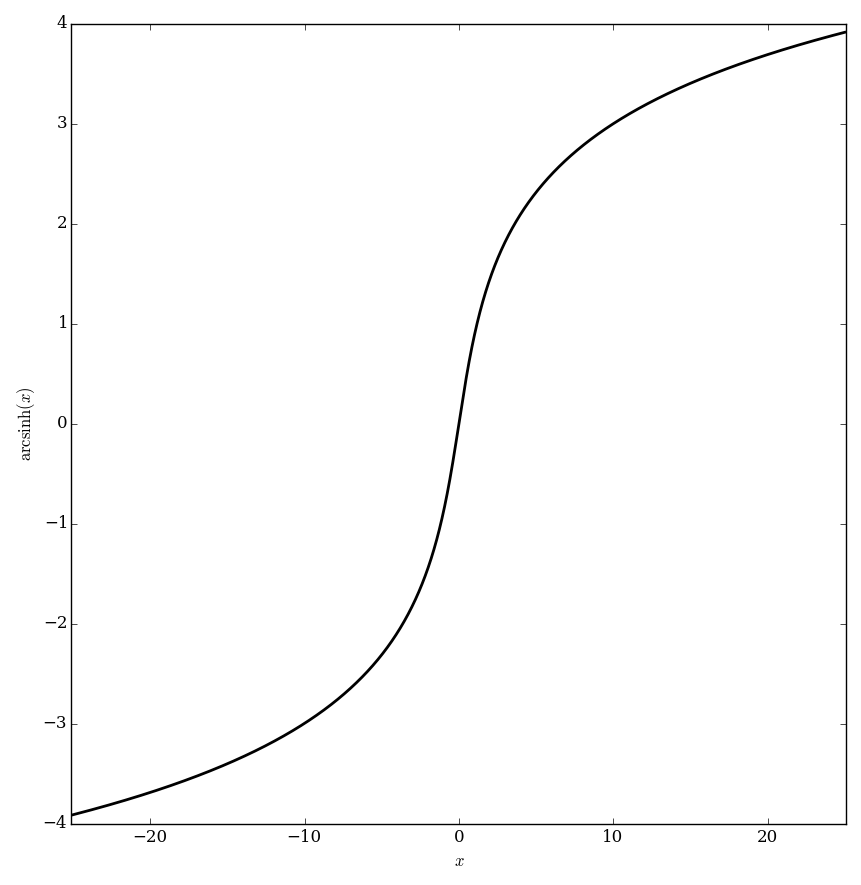
The inverse hyperbolic sine function $\mathrm{arcsinh} \colon \mathbb{R} \rightarrow \mathbb{R}$ function is the inverse function of the hyperbolic sine function.
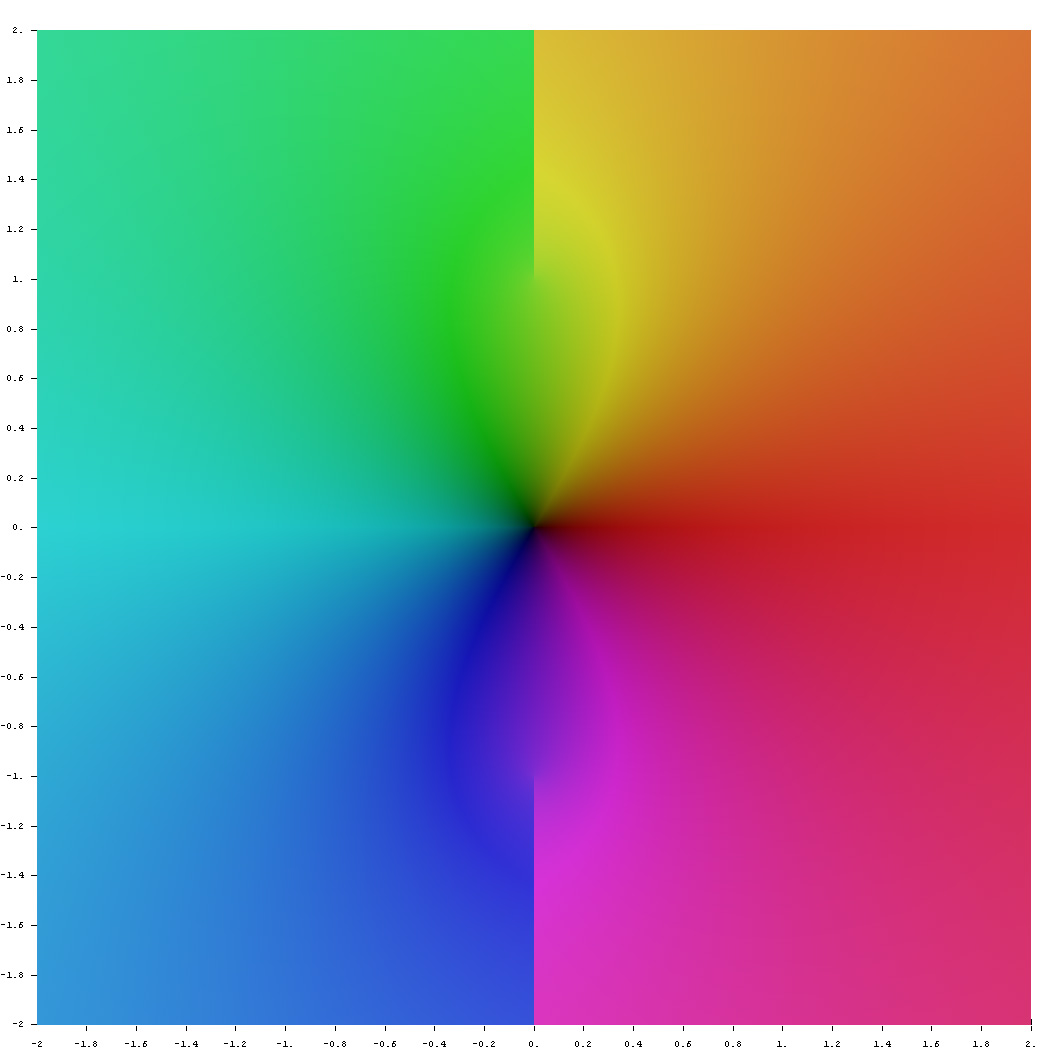
Domain coloring of analytic continuation of $\mathrm{arcsinh}$.