Difference between revisions of "Tanhc"
From specialfunctionswiki
| Line 10: | Line 10: | ||
=Properties= | =Properties= | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<center>{{:*-c functions footer}}</center> | <center>{{:*-c functions footer}}</center> | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 08:02, 8 June 2016
The $\mathrm{tanhc}$ function is defined by $$\mathrm{tanhc}(z) = \dfrac{\mathrm{tanh}(z)}{z}.$$
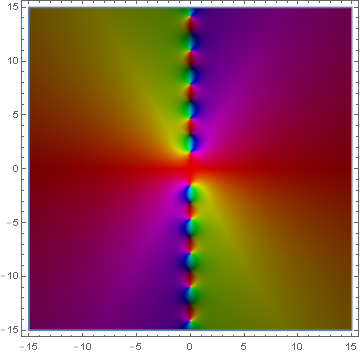
Domain coloring of analytic continuation of $\mathrm{tanhc}(z)$.