|
|
| Line 15: |
Line 15: |
| | | | |
| | =Properties= | | =Properties= |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| + | [[Relationship between the exponential integral and upper incomplete gamma function]] |
| − | <strong>Theorem:</strong> The exponential integral $E_1$ has series representation
| |
| − | $$E_1(z)=-\gamma-\log z - \displaystyle\sum_{k=1}^{\infty} \dfrac{(-1)^kz^k}{kk!}, \quad |\mathrm{arg}(z)|<\pi,$$
| |
| − | where $\gamma$ denotes the [[Euler-Mascheroni constant]].
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem (Symmetry):</strong> The following symmetry relation holds:
| |
| − | $$E_n(\overline{z})=\overline{E_n(z)}.$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem (Recurrence):</strong> The following recurrence holds:
| |
| − | $$E_{n+1}(z) = \dfrac{1}{n}[e^{-z}-zE_n(z)];(n=1,2,3,\ldots).$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem ([[Continued fraction]]):</strong> The following formula holds:
| |
| − | $$E_n(z)=e^{-z} \left( \dfrac{1}{z+} \dfrac{n}{1+} \dfrac{1}{z+} \dfrac{n+1}{1+} \dfrac{2}{z+} \ldots \right); |\mathrm{arg} z|<\pi.$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> The following value is known:
| |
| − | $$E_n(0)=\dfrac{1}{n-1}; n>1.$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem:</strong> The following closed form expression is known:
| |
| − | $$E_0(z)=\dfrac{e^{-z}}{z}.$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | <div class="toccolours mw-collapsible mw-collapsed">
| |
| − | <strong>Theorem (Derivative):</strong> $$\dfrac{d}{dz} E_n(z) = -E_{n-1}(z); n=1,2,3,\ldots$$
| |
| − | <div class="mw-collapsible-content">
| |
| − | <strong>Proof:</strong> █
| |
| − | </div>
| |
| − | </div>
| |
| − | | |
| − | {{:Relationship between the exponential integral and upper incomplete gamma function}}
| |
| | | | |
| | =Videos= | | =Videos= |
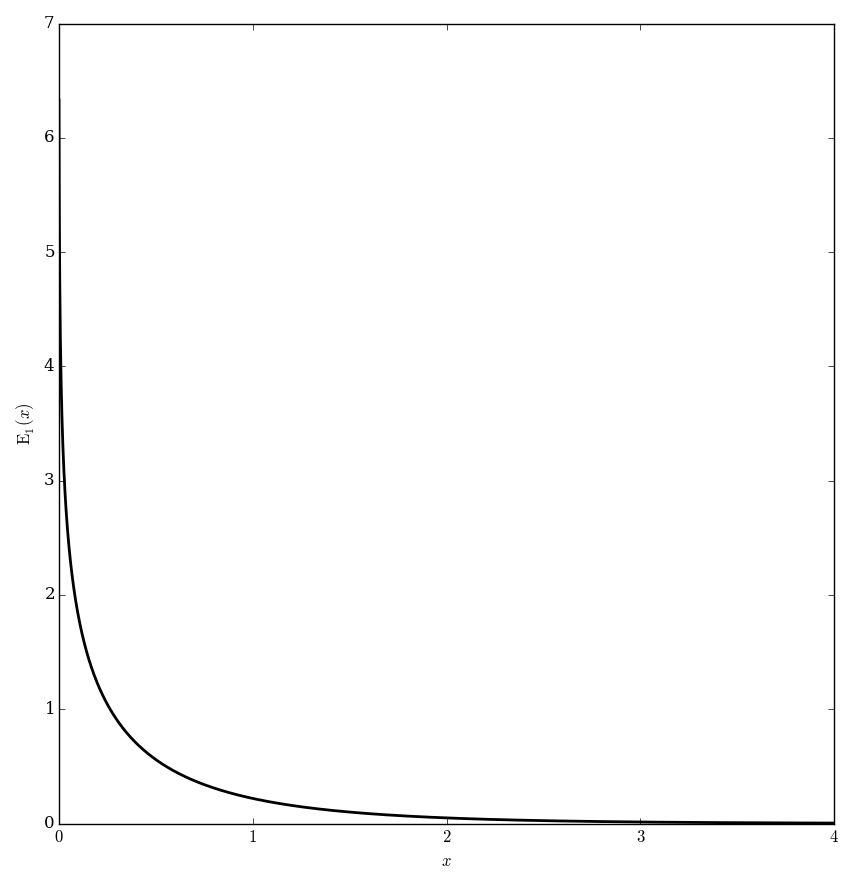
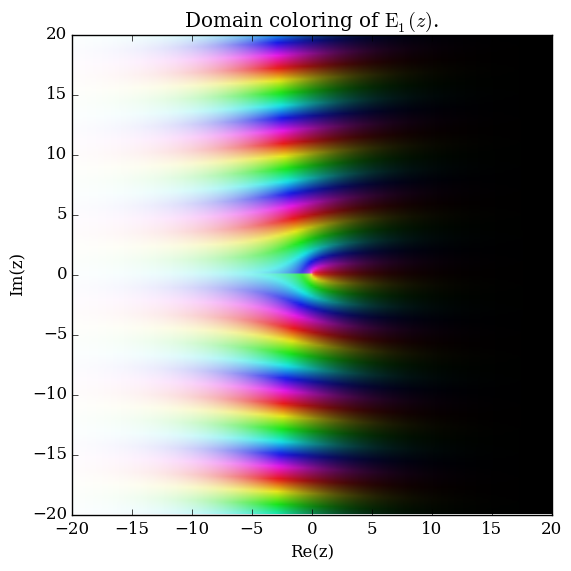
The exponential integral functions $E_n$ are defined by
$$E_1(z) = \displaystyle\int_1^{\infty} \dfrac{e^{-t}}{t} \mathrm{d}t, \quad \left|\mathrm{arg \hspace{2pt}}z\right|<\pi,$$
and
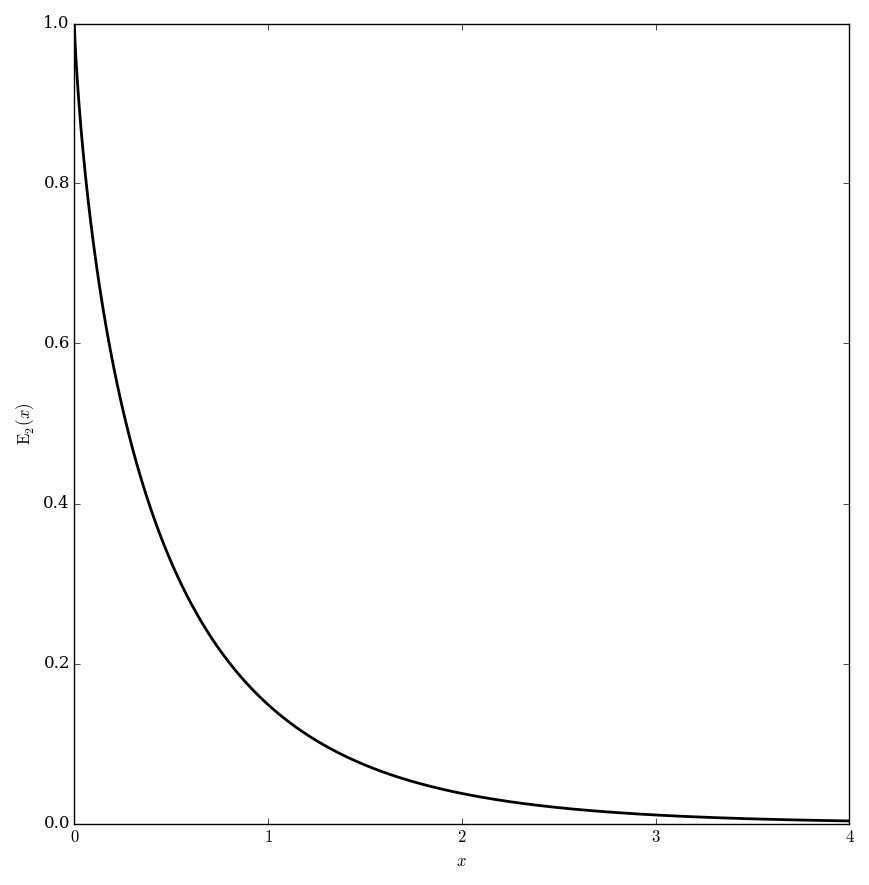
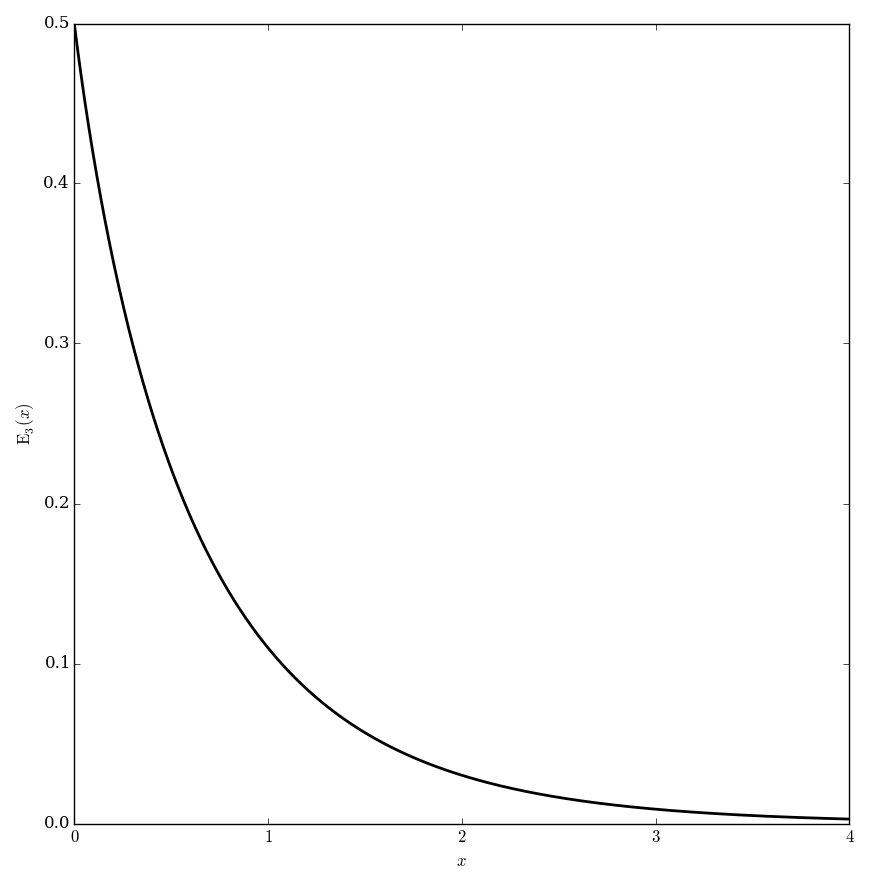
$$E_n(z)=\displaystyle\int_1^{\infty} \dfrac{e^{-zt}}{t^n} \mathrm{d}t.$$