Difference between revisions of "Riemann zeta"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
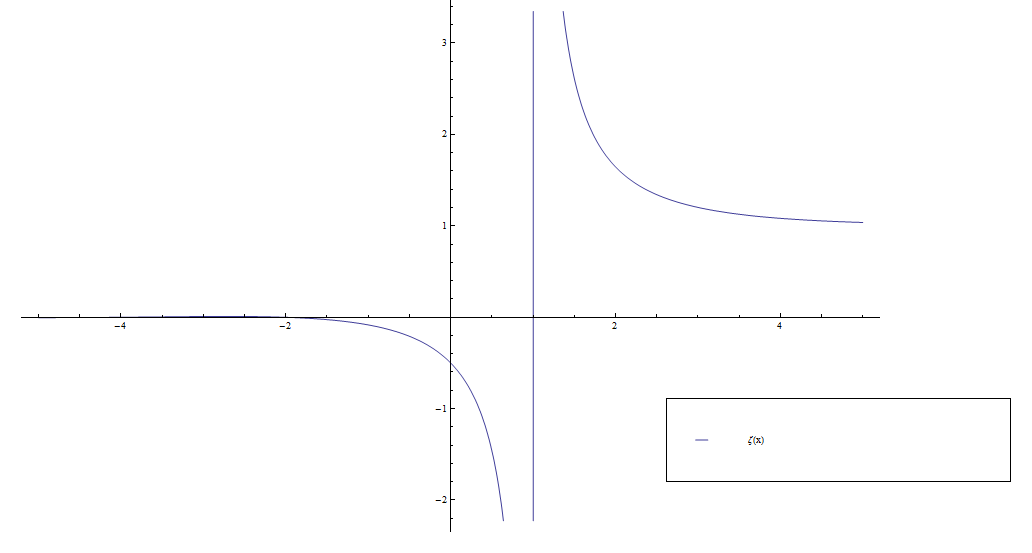
Consider the function $\zeta$ defined by the series | Consider the function $\zeta$ defined by the series | ||
$$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z},$$ | $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z},$$ | ||
| Line 16: | Line 17: | ||
=Videos= | =Videos= | ||
[https://www.youtube.com/watch?v=ZlYfEqdlhk0&list=PL32446FDD4DA932C9 Riemann Zeta function playlist]<br /> | [https://www.youtube.com/watch?v=ZlYfEqdlhk0&list=PL32446FDD4DA932C9 Riemann Zeta function playlist]<br /> | ||
| − | |||
| − | |||
| − | |||
=External links= | =External links= | ||
| Line 28: | Line 26: | ||
*[http://empslocal.ex.ac.uk/people/staff/mrwatkin//zeta/devlin.pdf How Euler discovered the zeta function] | *[http://empslocal.ex.ac.uk/people/staff/mrwatkin//zeta/devlin.pdf How Euler discovered the zeta function] | ||
*[http://www.dtc.umn.edu/~odlyzko/zeta_tables/ Andrew Odlyzko: Tables of zeros of the Riemann zeta function] | *[http://www.dtc.umn.edu/~odlyzko/zeta_tables/ Andrew Odlyzko: Tables of zeros of the Riemann zeta function] | ||
| + | |||
| + | =References= | ||
| + | * {{BookReference|The Zeta-Function of Riemann|1930|Edward Charles Titchmarsh|next=Euler product for Riemann zeta}}: § Introduction (1) | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 19:47, 9 June 2016
Consider the function $\zeta$ defined by the series $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z},$$ which is valid for $\mathrm{Re}(z)>1$.
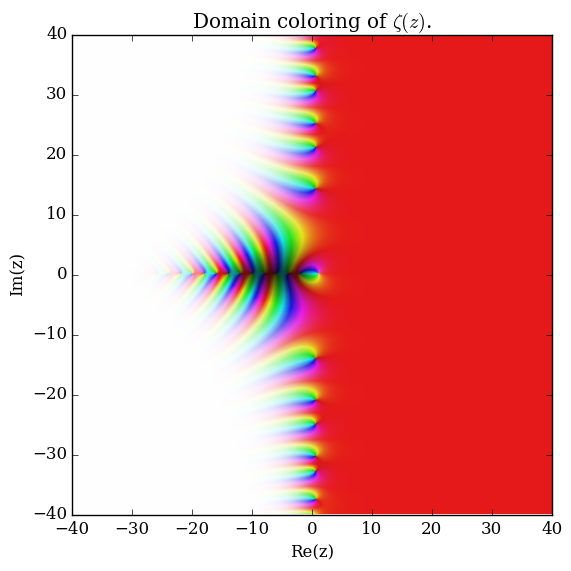
Domain coloring of $\zeta$.
Properties
Euler product for Riemann zeta Laurent series of the Riemann zeta function Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
Videos
Riemann Zeta function playlist
External links
- 15 Videos about the Riemann $\zeta$ function
- English translation of Riemann's paper "On the number of prime numbers less than a given quantity"
- Evaluating $\zeta(2)$
- The Riemann Hypothesis: How to make $1 Million Without Getting Out of Bed
- The Riemann Hypothesis: FAQ and resources
- How Euler discovered the zeta function
- Andrew Odlyzko: Tables of zeros of the Riemann zeta function
References
- 1930: Edward Charles Titchmarsh: The Zeta-Function of Riemann ... (next): § Introduction (1)