Difference between revisions of "Modified Bessel I"
From specialfunctionswiki
| Line 15: | Line 15: | ||
[[Relationship between Bessel I sub n and Bessel J sub n]]<br /> | [[Relationship between Bessel I sub n and Bessel J sub n]]<br /> | ||
[[Relationship between Airy Bi and modified Bessel I]]<br /> | [[Relationship between Airy Bi and modified Bessel I]]<br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<center>{{:Bessel functions footer}}</center> | <center>{{:Bessel functions footer}}</center> | ||
Revision as of 20:12, 9 June 2016
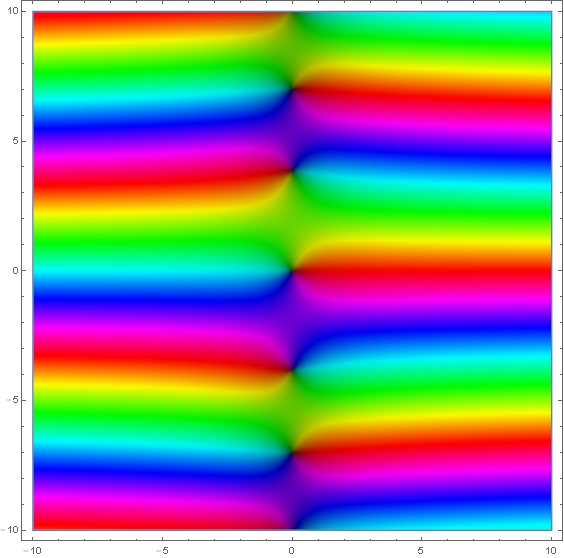
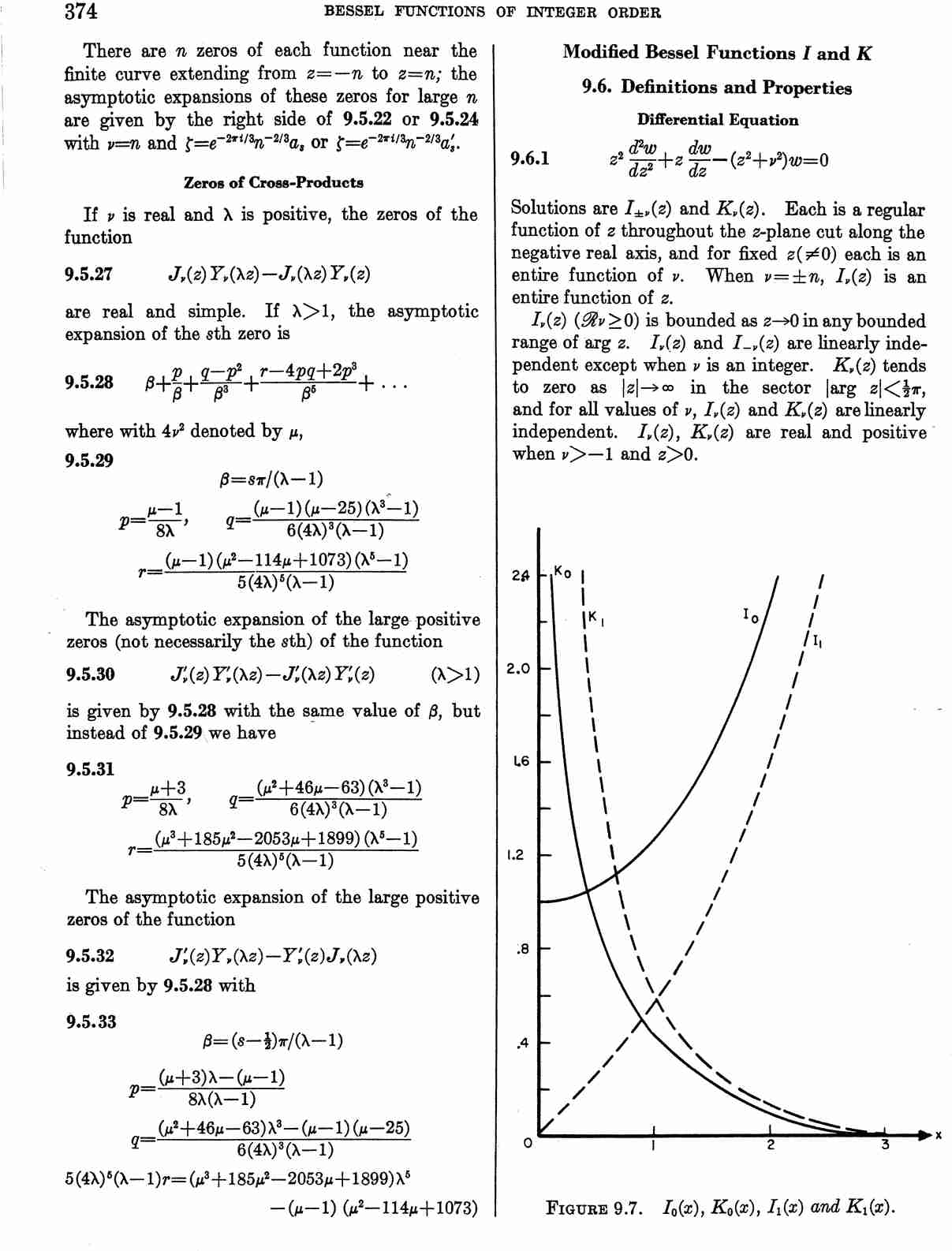
The modified Bessel function of the first kind is defined by $$I_{\nu}(z)=i^{-\nu}J_{\nu}(iz),$$ where $J_{\nu}$ is the Bessel function of the first kind.
Domain coloring of analytic continuation of $I_1(z)$.
Properties
Relationship between Bessel I sub -1/2 and cosh
Relationship between Bessel I sub 1/2 and sinh
Relationship between Bessel I sub n and Bessel J sub n
Relationship between Airy Bi and modified Bessel I
Bessel $I_{\nu}$