Difference between revisions of "Bessel Y"
From specialfunctionswiki
| Line 20: | Line 20: | ||
=References= | =References= | ||
[http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0021%7CLOG_0023 Bessel's functions of the second order - C.V. Coates]<br /> | [http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0021%7CLOG_0023 Bessel's functions of the second order - C.V. Coates]<br /> | ||
| − | + | ||
| + | {{:Bessel functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
| − | |||
| − | |||
Revision as of 19:14, 10 June 2016
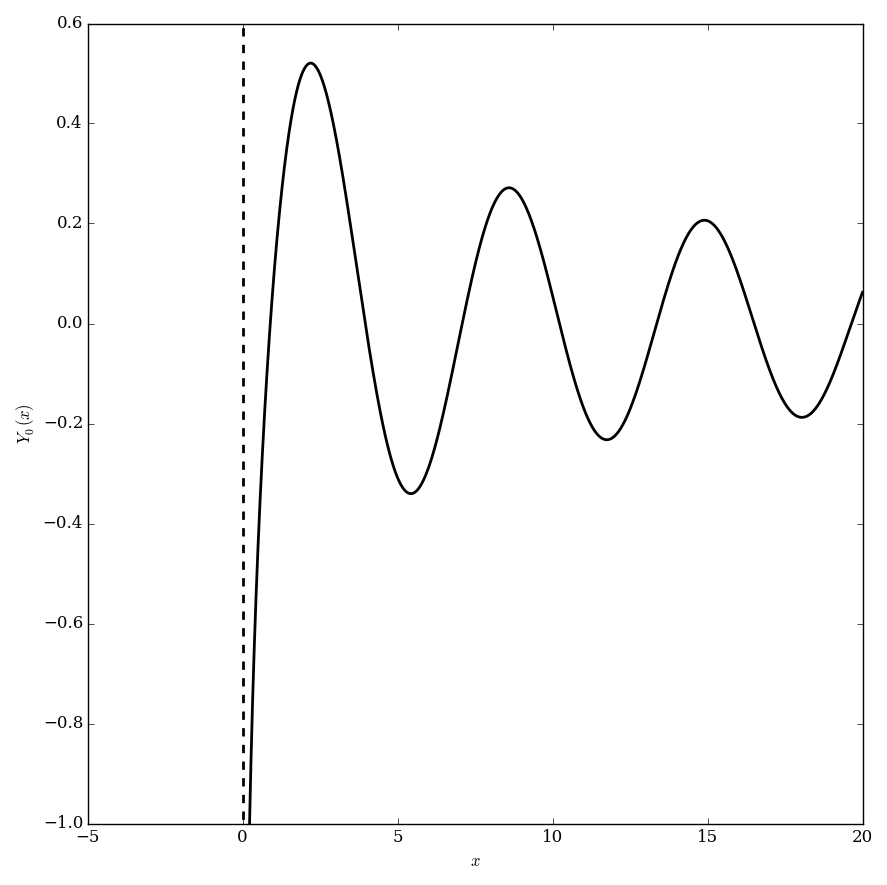
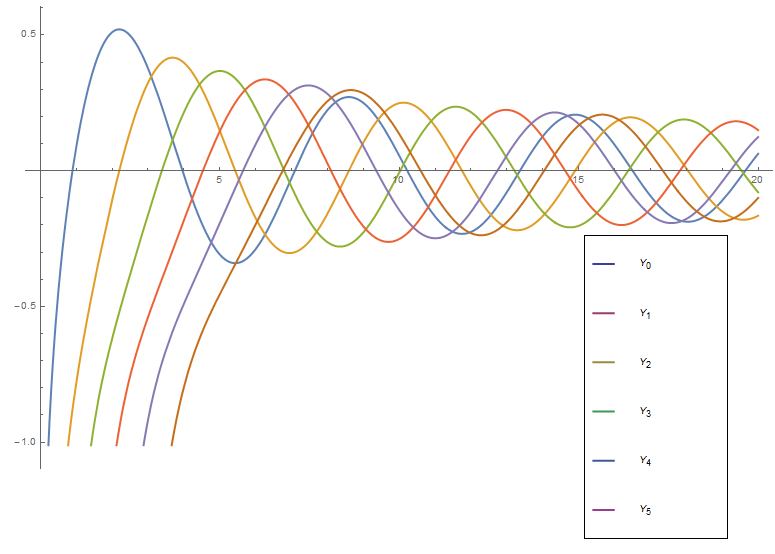
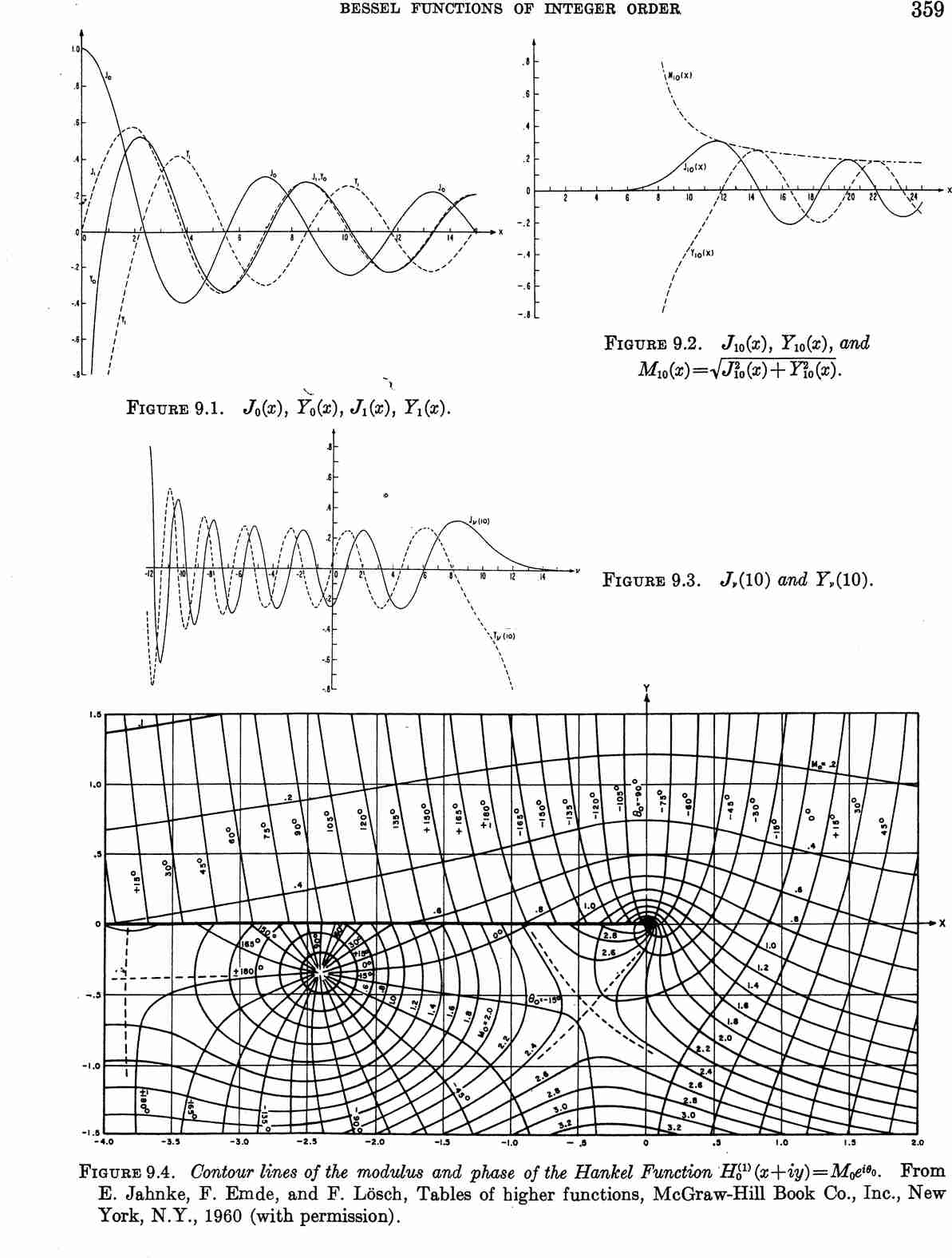
Bessel functions of the second kind $Y_{\nu}$ are defined via the formula $$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$ Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.
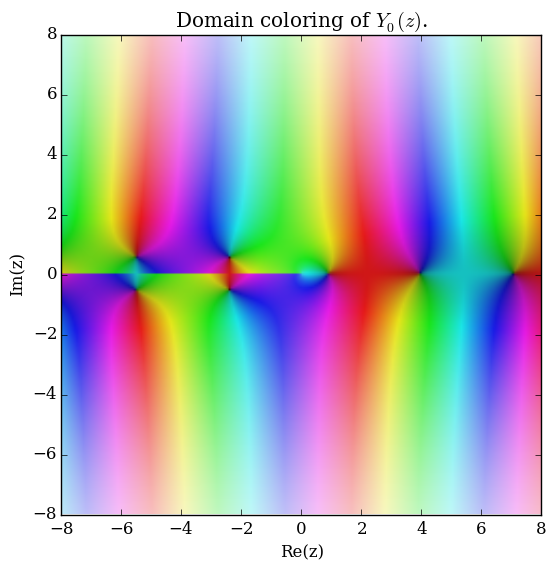
Domain coloring of $Y_0$.
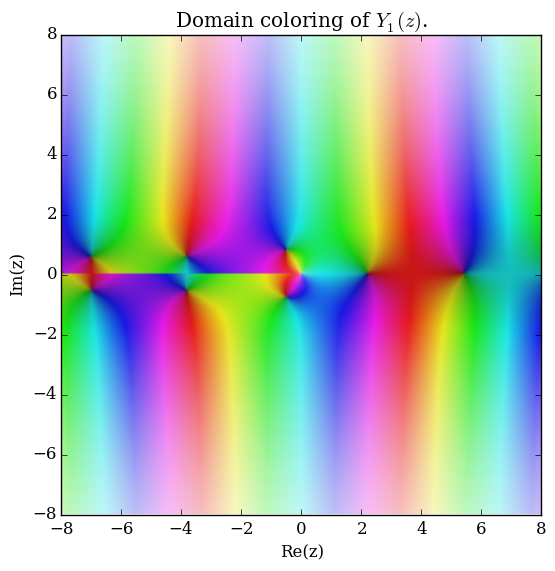
Domain coloring of $Y_1$.
Bessel functions from Abramowitz&Stegun
Properties
References
Bessel's functions of the second order - C.V. Coates