Difference between revisions of "Gamma"
(→Properties) |
|||
| Line 19: | Line 19: | ||
[[Factorial property of gamma]]<br /> | [[Factorial property of gamma]]<br /> | ||
[[Gamma at positive integers]]<br /> | [[Gamma at positive integers]]<br /> | ||
| − | |||
[[Relationship between Hurwitz zeta and gamma function]]<br /> | [[Relationship between Hurwitz zeta and gamma function]]<br /> | ||
[[Gamma-Sine Relation]]<br /> | [[Gamma-Sine Relation]]<br /> | ||
Revision as of 03:31, 12 June 2016
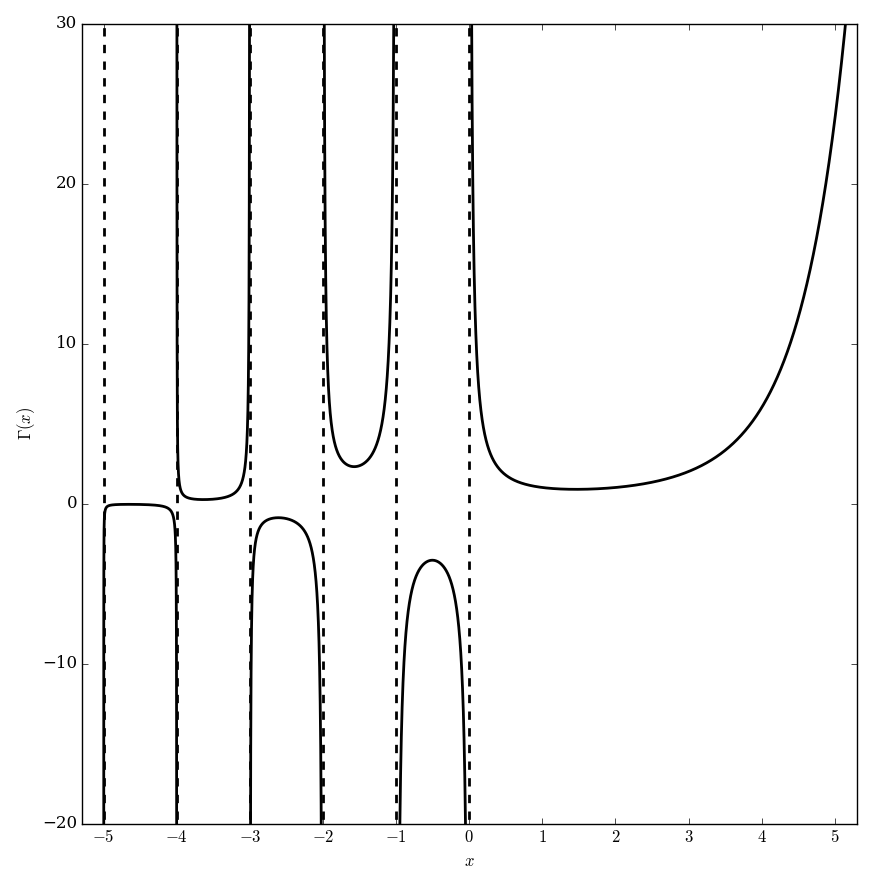
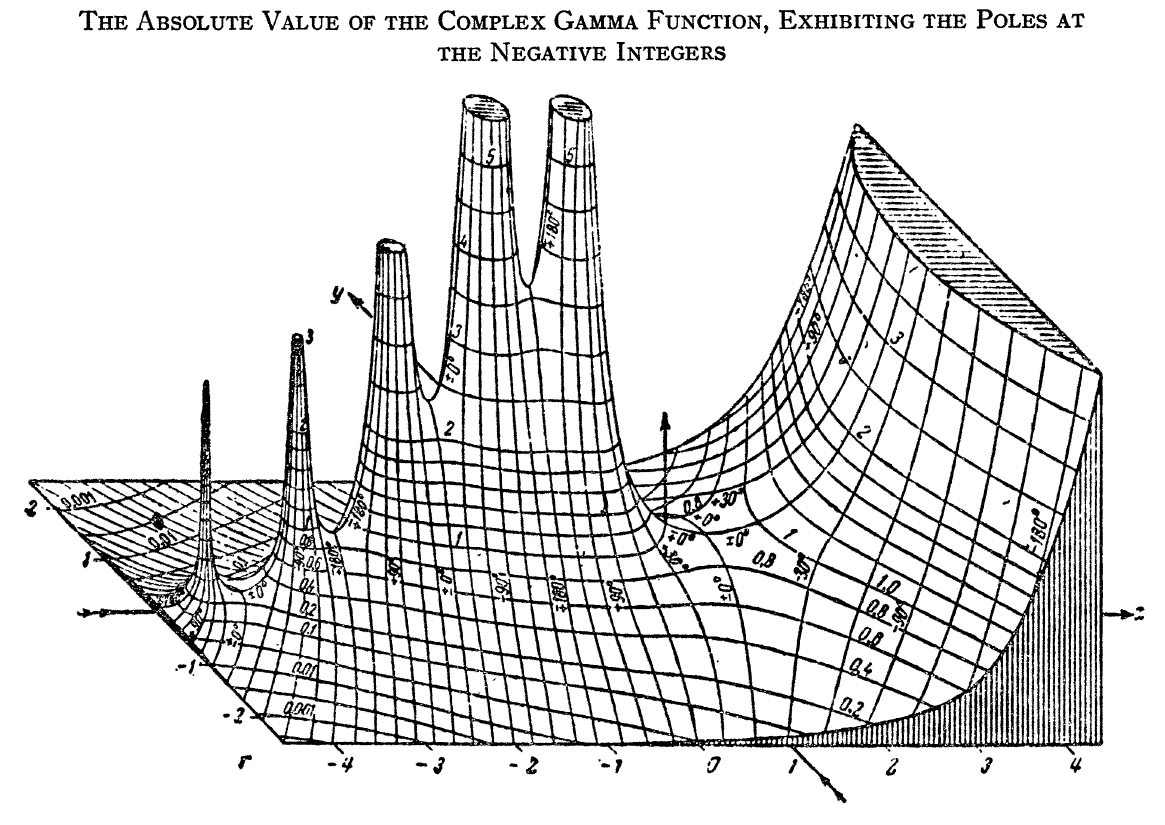
The gamma function $\Gamma \colon \mathbb{C} \setminus \{0,-1,-2,\ldots\} \rightarrow \mathbb{C}$ is the function initially defined for $\mathrm{Re}(z)>0$ by the integral by the formula $$\Gamma(x)=\displaystyle\int_0^{\infty} \xi^{x-1}e^{-\xi} \mathrm{d}\xi.$$ The analytic continuation of $\Gamma$ leads to a meromorphic function with poles at the negative integers.
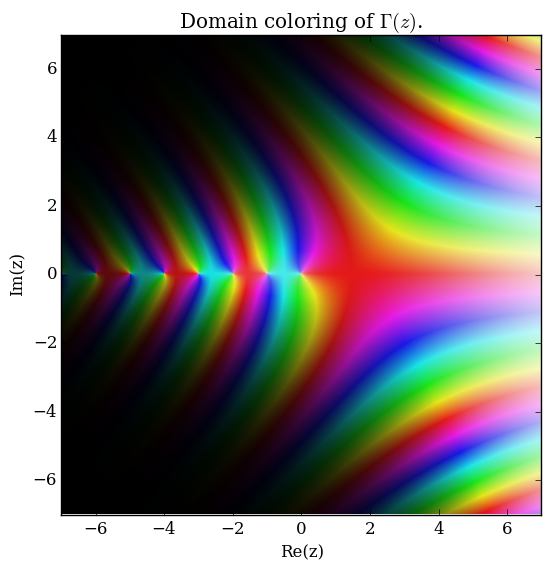
Domain coloring of $\Gamma$.
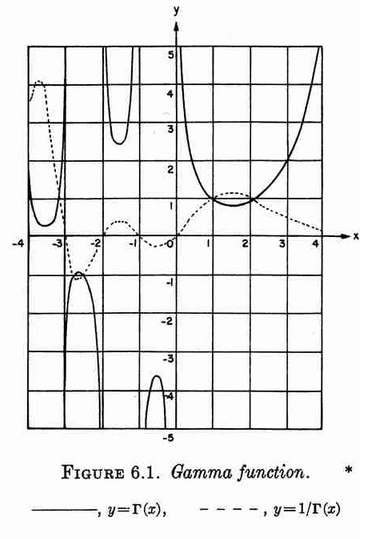
Plot of $\Gamma$ and $\dfrac{1}{\Gamma}$ from Abramowitz&Stegun.
Contents
Properties
Gamma(z) as integral of a power of log(1/t) for Re(z) greater than 0
Gamma function written as a limit of a factorial, exponential, and a rising factorial
Gamma function written as infinite product
Value of Gamma(1)
Factorial property of gamma
Gamma at positive integers
Relationship between Hurwitz zeta and gamma function
Gamma-Sine Relation
Bohr-Mollerup theorem
Videos
Gamma Function (playlist)
The Gamma Function: intro (5)
Gamma Integral Function - Introduction
Gamma function
Mod-04 Lec-09 Analytic continuation and the gamma function (Part I)
gamma function - Part 1
Beta Function, Gamma Function and their Properties
What's the Gamma Function?
euler gamma function
Thermodynamics 19 a : Gamma Function 1/2
The Gamma Function: why 0!=1 (5)
Gamma Function Of One-Half: Part 1
Gamma Function Of One-Half: Part 2
Gamma function at 1/2
Contour Integral Definition of the Gamma Function
See Also
Loggamma
Polygamma
Reciprocal gamma
References
- 1920: Edmund Taylor Whittaker and George Neville Watson: A course of modern analysis ... (previous) ... (next): $\S 12 \cdot 1$
- 1953: Harry Bateman: Higher Transcendental Functions Volume I ... (next): §1.1 (1)
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 6.1.1
The sine product formula and the gamma function
Leonhard Euler's Integral: A Historical Profile of the Gamma Function