Difference between revisions of "Prime zeta P"
From specialfunctionswiki
(→References) |
|||
| Line 16: | Line 16: | ||
=References= | =References= | ||
* {{PaperReference|The Sums of the Series of the Reciprocals of the Prime Numbers and of Their Powers|1881|Charles Watkins Merrifield}} | * {{PaperReference|The Sums of the Series of the Reciprocals of the Prime Numbers and of Their Powers|1881|Charles Watkins Merrifield}} | ||
| + | * {{PaperReference|On the Sums of the Inverse Powers of the Prime Numbers|1891|James Whitbread Lee Glaisher}} | ||
Fröberg, Carl-Erik . On the prime zeta function. Nordisk Tidskr. Informationsbehandling (BIT) 8 1968 187--202.<br /> | Fröberg, Carl-Erik . On the prime zeta function. Nordisk Tidskr. Informationsbehandling (BIT) 8 1968 187--202.<br /> | ||
[http://math.stackexchange.com/questions/49383/how-does-sum-px-p-s-grow-asymptotically-for-textres-1/49434#49434 How does ∑p<xp−s grow asymptotically for Re(s)<1?] <br /> | [http://math.stackexchange.com/questions/49383/how-does-sum-px-p-s-grow-asymptotically-for-textres-1/49434#49434 How does ∑p<xp−s grow asymptotically for Re(s)<1?] <br /> | ||
| − | |||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 19:22, 15 June 2016
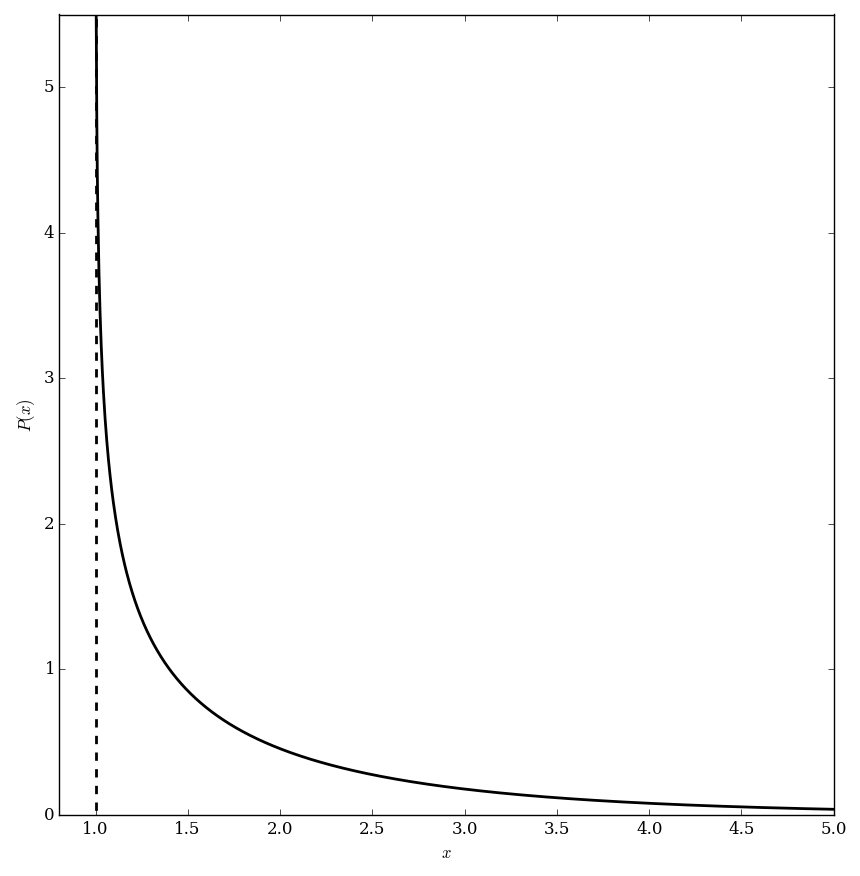
The prime zeta function is defined by $$P(z) = \displaystyle\sum_{p \mathrm{\hspace{2pt} prime}} \dfrac{1}{p^z},$$ where $\mathrm{Re}(z)>1$. It can be extended outside of this domain via analytic continuation.
Properties
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
References
- Charles Watkins Merrifield: The Sums of the Series of the Reciprocals of the Prime Numbers and of Their Powers (1881)
- James Whitbread Lee Glaisher: On the Sums of the Inverse Powers of the Prime Numbers (1891)
Fröberg, Carl-Erik . On the prime zeta function. Nordisk Tidskr. Informationsbehandling (BIT) 8 1968 187--202.
How does ∑p<xp−s grow asymptotically for Re(s)<1?