Difference between revisions of "Cosine integral"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
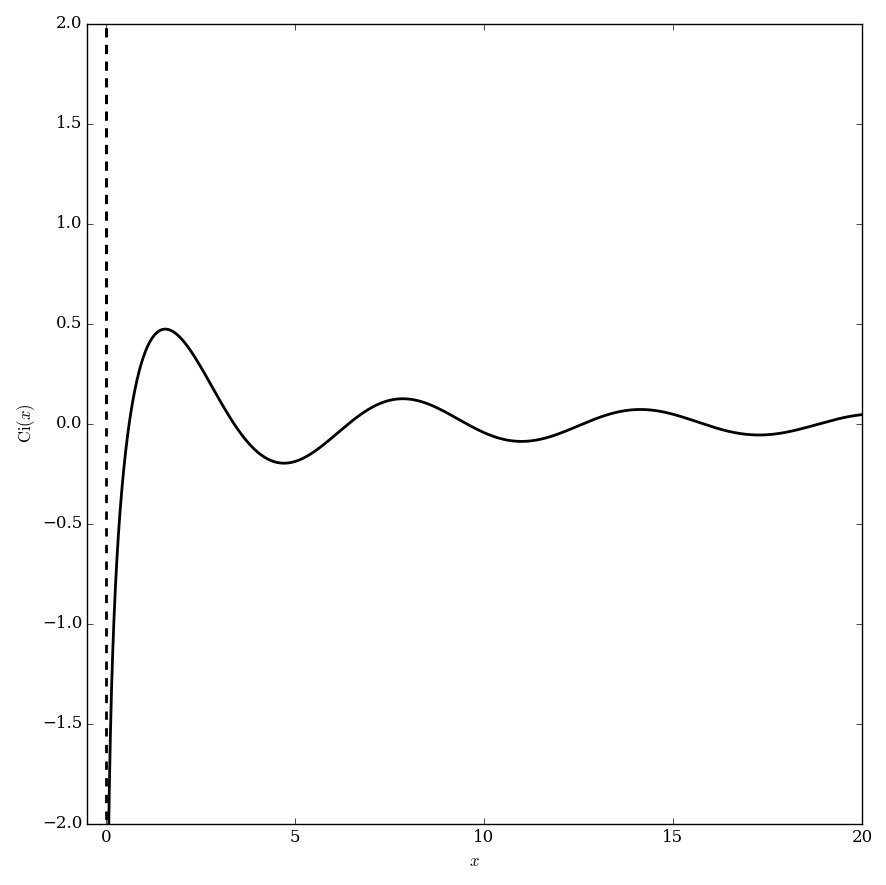
The cosine integral is defined by | The cosine integral is defined by | ||
$$\mathrm{Ci}(z) = -\displaystyle\int_z^{\infty} \dfrac{\cos t}{t} \mathrm{d}t, \quad |\mathrm{arg} z|<\pi.$$ | $$\mathrm{Ci}(z) = -\displaystyle\int_z^{\infty} \dfrac{\cos t}{t} \mathrm{d}t, \quad |\mathrm{arg} z|<\pi.$$ | ||
Revision as of 19:45, 19 June 2016
The cosine integral is defined by $$\mathrm{Ci}(z) = -\displaystyle\int_z^{\infty} \dfrac{\cos t}{t} \mathrm{d}t, \quad |\mathrm{arg} z|<\pi.$$
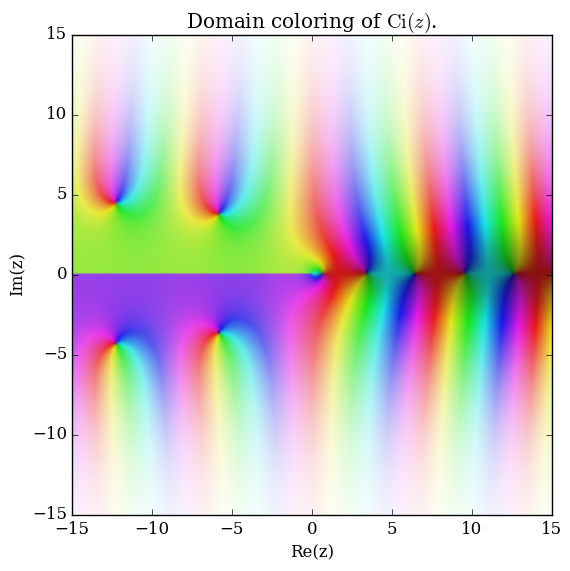
Domain coloring of $\mathrm{Ci}$.
Relationship to other functions
Relationship between exponential integral Ei, cosine integral, and sine integral
Videos
Laplace transform of cosine integral