Difference between revisions of "Möbius"
| Line 25: | Line 25: | ||
=References= | =References= | ||
| − | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Reciprocal of Riemann zeta as a sum of Möbius function for Re(z) greater than 1}}: 24.3.1 I.A. | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=findme|next=Reciprocal of Riemann zeta as a sum of Möbius function for Re(z) greater than 1}}: $24.3.1 \mathrm{I}.A.$ |
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 01:35, 22 June 2016
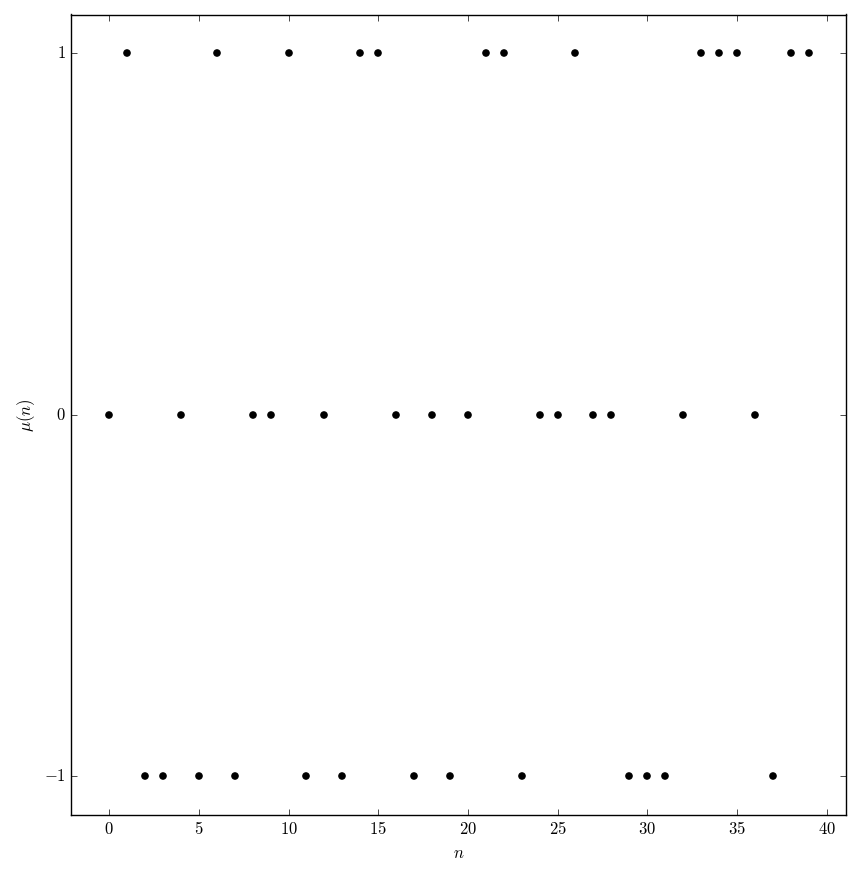
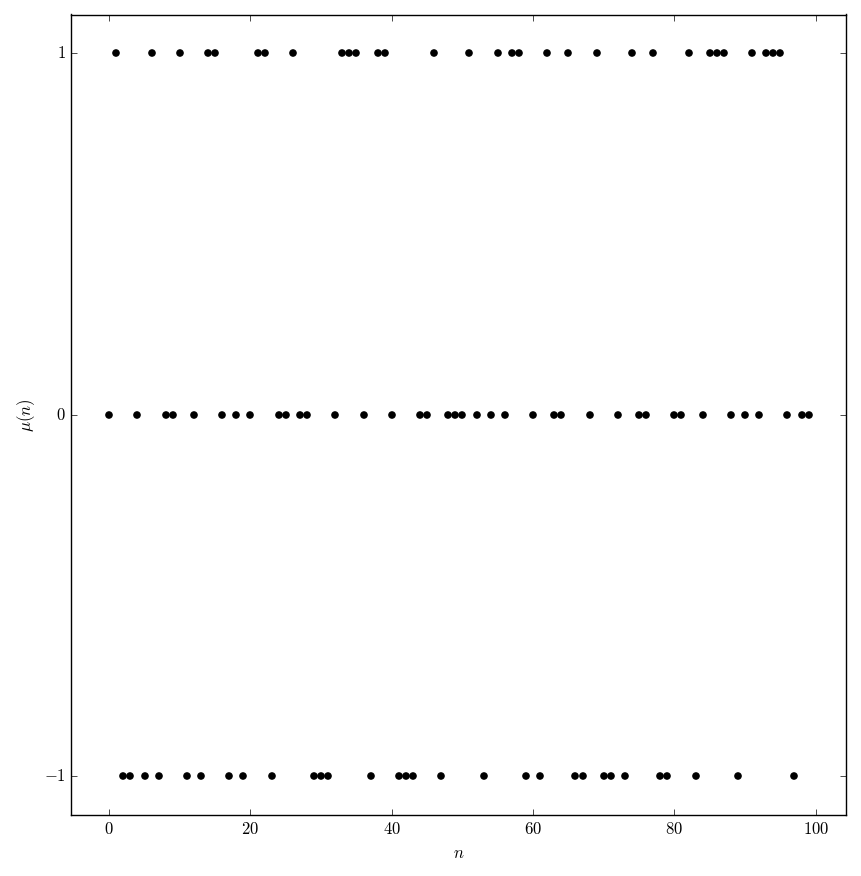
The Möbius function is the function $\mu$ defined by the formula $$\mu(n) = \left\{ \begin{array}{ll} 1 &; n \mathrm{\hspace{2pt}is\hspace{2pt}a\hspace{2pt}squarefree\hspace{2pt}positive\hspace{2pt}integer\hspace{2pt}with\hspace{2pt}even\hspace{2pt}number\hspace{2pt}of\hspace{2pt}prime\hspace{2pt}factors} \\ -1 &; n \mathrm{\hspace{2pt}is\hspace{2pt}a\hspace{2pt}squarefree\hspace{2pt}positive\hspace{2pt}integer\hspace{2pt}with\hspace{2pt}odd\hspace{2pt}number\hspace{2pt}of\hspace{2pt}prime\hspace{2pt}factors} \\ 0 &; n\mathrm{\hspace{2pt}has\hspace{2pt}a\hspace{2pt}square\hspace{2pt}divisor}. \end{array} \right.$$
Graph of $\mu$ on $[0,40]$.
Graph of $\mu$ on $[0,100]$.
Properties
Reciprocal of Riemann zeta as a sum of Möbius function for Re(z) greater than 1
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta
Videos
Mobius Function Example
Möbius Function - Introduction
Möbius Function - Merten's function
Number Theory 27: Mobius function is multiplicative
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $24.3.1 \mathrm{I}.A.$
