Difference between revisions of "Coth"
From specialfunctionswiki
| Line 1: | Line 1: | ||
| + | __NOTOC__ | ||
The hyperbolic cotangent is defined by | The hyperbolic cotangent is defined by | ||
$$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)},$$ | $$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)},$$ | ||
Revision as of 17:38, 24 June 2016
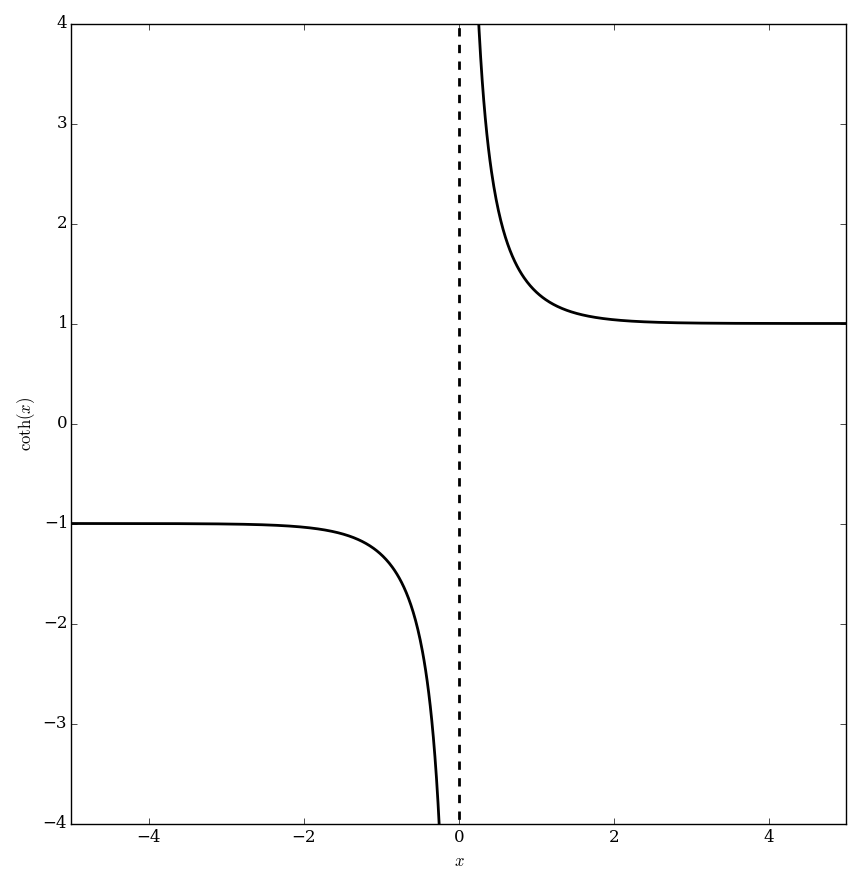
The hyperbolic cotangent is defined by $$\mathrm{coth}(z)=\dfrac{1}{\tanh(z)},$$ where $\tanh$ denotes the hyperbolic tangent function.
Plot of $\mathrm{coth}$ on $[-5,5]$.
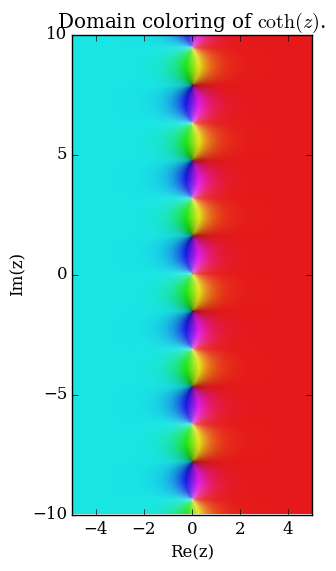
Domain coloring of $\mathrm{coth}$.
Properties
Derivative of coth
Antiderivative of coth
Relationship between coth and csch
Relationship between coth and cot
Relationship between cot and coth
Relationship between csc, Gudermannian, and coth
Relationship between coth, inverse Gudermannian, and csc
Videos
Calculus I - Derivative of Hyperbolic Cotangent Function coth(x) - Proof
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.5.6
