Difference between revisions of "Exponential integral Ei"
From specialfunctionswiki
| Line 19: | Line 19: | ||
=References= | =References= | ||
| + | * {{PaperReference|On certain definite integrals involving the exponential-integral|1881|James Whitbread Lee Glaisher|next=findme}} | ||
* {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Exponential integral E|next=Logarithmic integral}}: $5.1.2$ | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Exponential integral E|next=Logarithmic integral}}: $5.1.2$ | ||
[http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0018%7CLOG_0048 On certain definite integrals involving the exponential-integral - J.W.L. Glaisher] | [http://gdz.sub.uni-goettingen.de/dms/load/img/?PID=PPN600494829_0018%7CLOG_0048 On certain definite integrals involving the exponential-integral - J.W.L. Glaisher] | ||
Revision as of 19:01, 7 August 2016
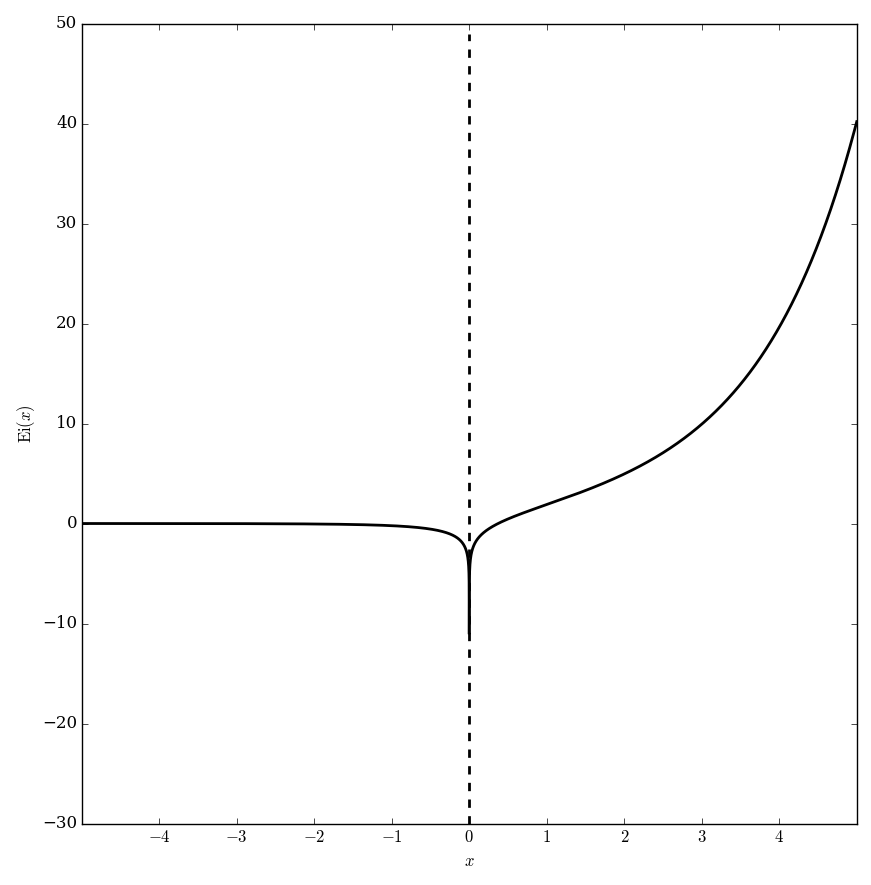
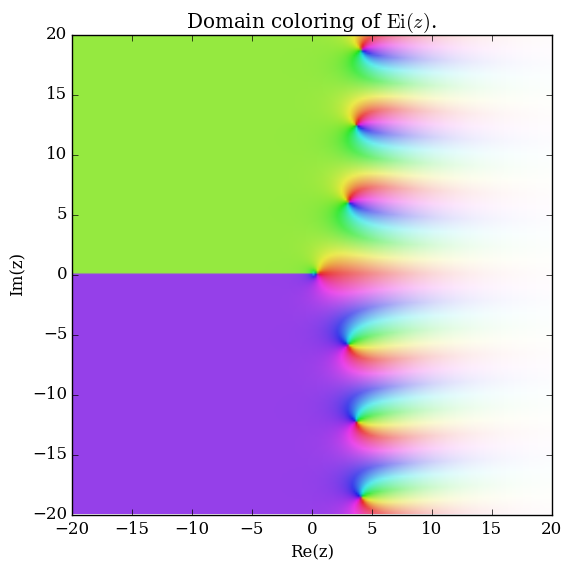
The exponential integral $\mathrm{Ei}$ is defined for $x>0$ by $$\mathrm{Ei}(x) = \int_{-\infty}^x \dfrac{e^t}{t} \mathrm{d}t.$$
Graph of $\mathrm{Ei}$.
Domain coloring of $\mathrm{Ei}$.
Properties
Relationship between logarithmic integral and exponential integral
Exponential integral Ei series
Relationship between exponential integral Ei, cosine integral, and sine integral
See Also
References
- James Whitbread Lee Glaisher: On certain definite integrals involving the exponential-integral (1881)... (next)
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $5.1.2$
On certain definite integrals involving the exponential-integral - J.W.L. Glaisher
Exp integral $\mathrm{Ei}$
