Difference between revisions of "Arcsin"
From specialfunctionswiki
| Line 13: | Line 13: | ||
[[Antiderivative of arcsin]] <br /> | [[Antiderivative of arcsin]] <br /> | ||
[[Relationship between arcsin and arccsc]] <br /> | [[Relationship between arcsin and arccsc]] <br /> | ||
| + | [[2F1(1/2,1/2;3/2;z^2)=arcsin(z)/z]]<br /> | ||
=Videos= | =Videos= | ||
Revision as of 02:45, 16 September 2016
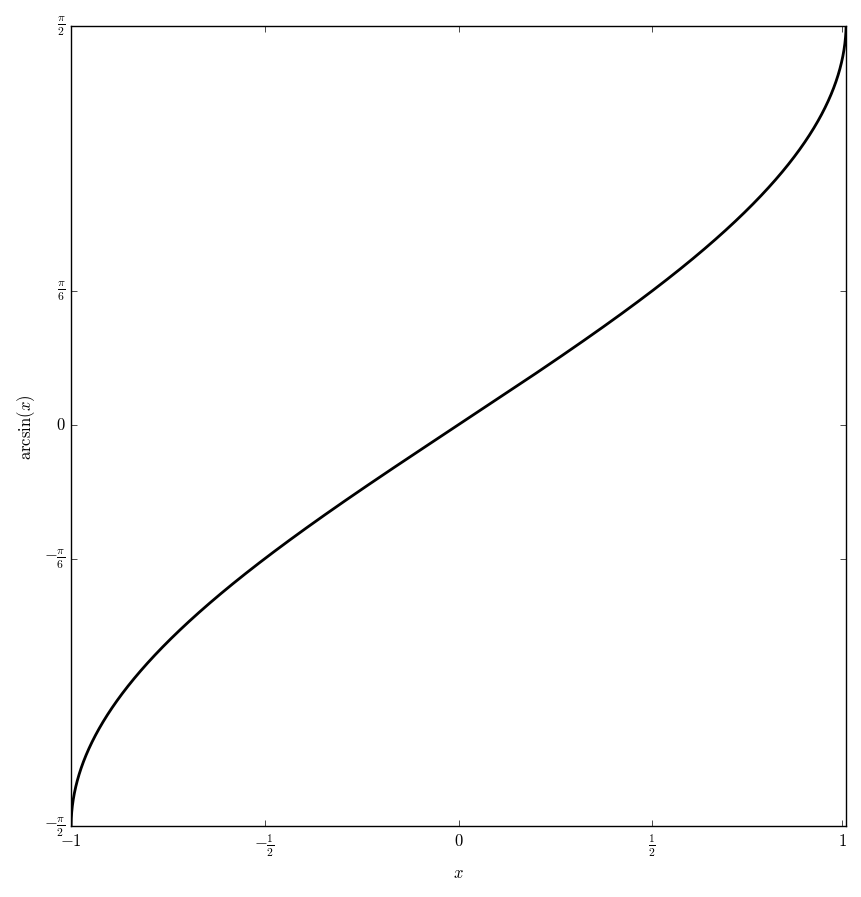
The function $\mathrm{arcsin} \colon [-1,1] \rightarrow \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$ is the inverse function of the sine function.
Graph of $\mathrm{arcsin}$ on $[-1,1]$.
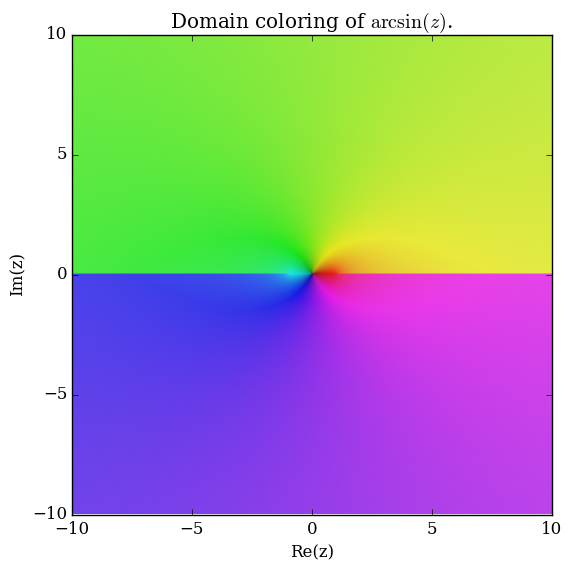
Domain coloring of $\mathrm{arcsin}$.
Properties
Derivative of arcsin
Antiderivative of arcsin
Relationship between arcsin and arccsc
2F1(1/2,1/2;3/2;z^2)=arcsin(z)/z
Videos
Inverse Trig Functions: Arcsin
Integrate x*arcsin(x)
What is arcsin(x)?
What is the inverse of arcsin(ln(x))?
See Also
References
On the function arc sin(x+iy)-Cayley
