Difference between revisions of "Hyperfactorial"
From specialfunctionswiki
| Line 4: | Line 4: | ||
<div align="center"> | <div align="center"> | ||
<gallery> | <gallery> | ||
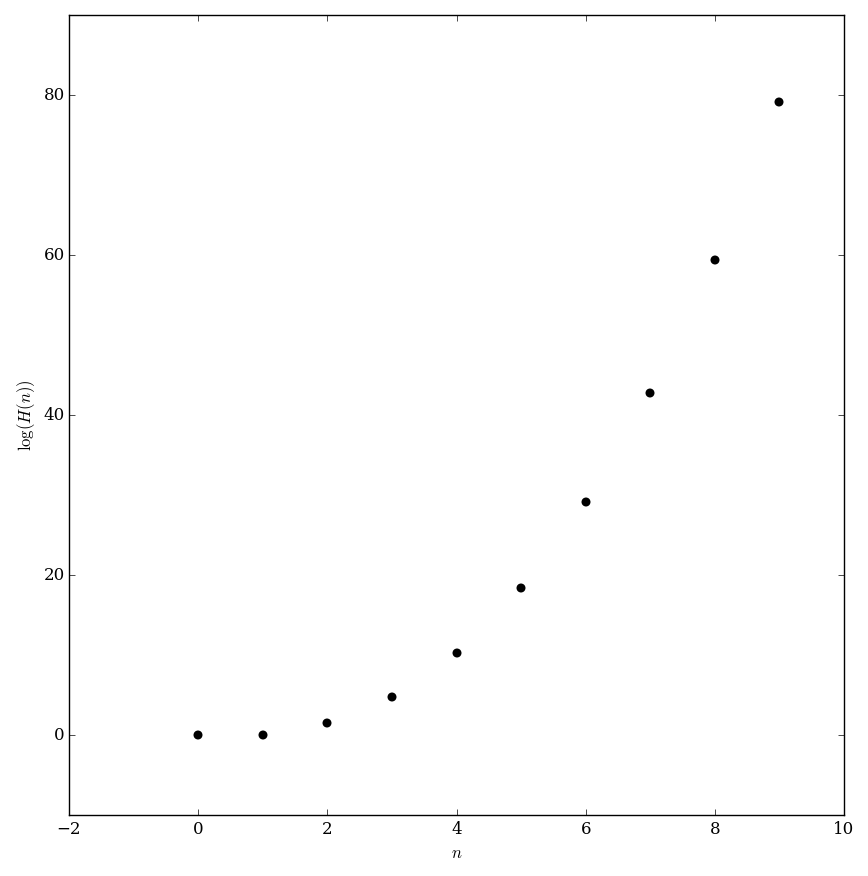
| − | File: | + | File:Loghyperfactorialplot.png|Plot of the [[logarithm]] of the hyperfactorial on $[0,10]$ (we plot the log because $H$ increases too fast to plot alone). |
File:Domain coloring hyperfactorial.png|[[Domain coloring]] of [[analytic continuation]] of $H(n)$. | File:Domain coloring hyperfactorial.png|[[Domain coloring]] of [[analytic continuation]] of $H(n)$. | ||
</gallery> | </gallery> | ||
Revision as of 19:22, 25 September 2016
The hyperfactorial is defined for integers $n=1,2,3,\ldots$ by the formula $$H(n)=\displaystyle\prod_{k=1}^n k^k.$$
Plot of the logarithm of the hyperfactorial on $[0,10]$ (we plot the log because $H$ increases too fast to plot alone).
- Domain coloring hyperfactorial.png
Domain coloring of analytic continuation of $H(n)$.