Difference between revisions of "Fresnel C"
From specialfunctionswiki
| Line 8: | Line 8: | ||
</gallery> | </gallery> | ||
</div> | </div> | ||
| + | |||
| + | =Properties= | ||
| + | [[Fresnel C is odd]]<br /> | ||
| + | [[Taylor series for Fresnel C]]<br /> | ||
| + | [[Fresnel C in terms of erf]]<br /> | ||
| + | [[Limiting value of Fresnel C]]<br /> | ||
=See Also= | =See Also= | ||
Revision as of 17:23, 5 October 2016
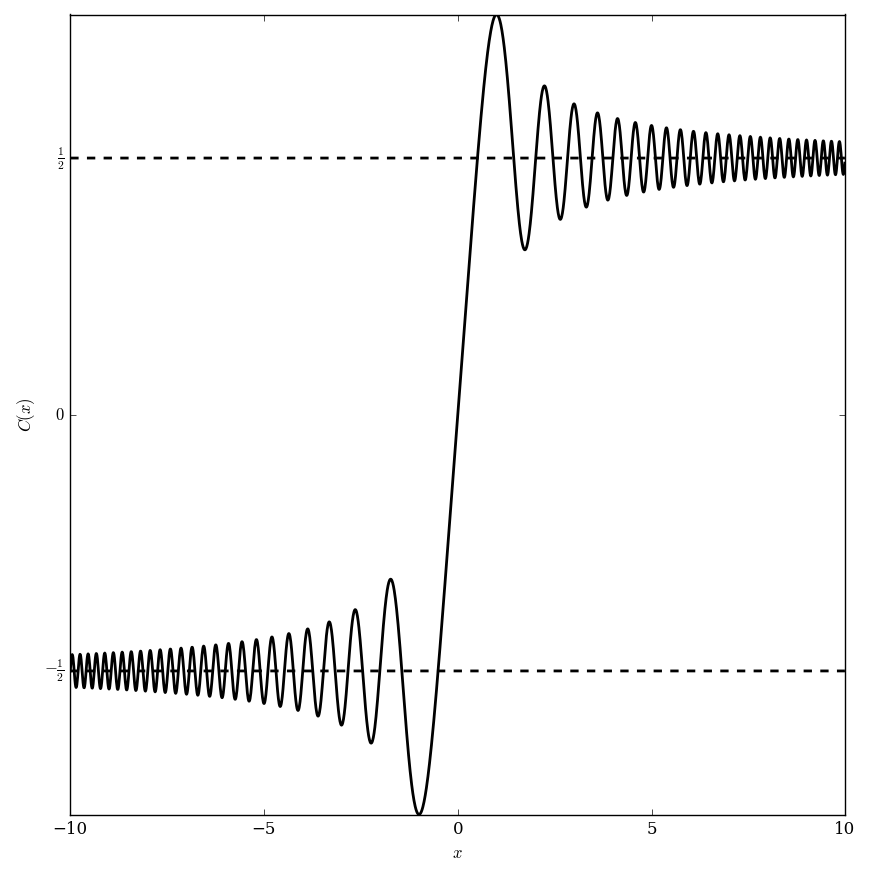
The Fresnel C function is defined by the formula $$C(x)=\int_0^x \cos(t^2) \mathrm{d}t.$$ (Note in Abramowitz&Stegun it is defined differently.)
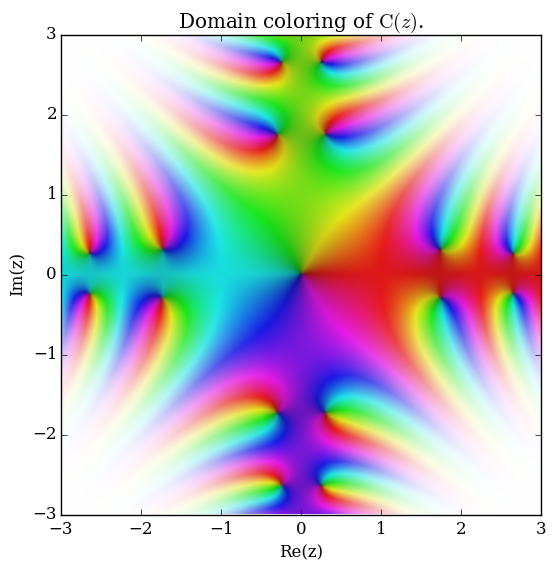
Domain coloring of Fresnel $C$.
Properties
Fresnel C is odd
Taylor series for Fresnel C
Fresnel C in terms of erf
Limiting value of Fresnel C
See Also
Videos
How to integrate cos(x^2) - The Fresnel Integral C(x) (2 December 2014)
Math and Physics: The Fresnel Integrals (12 May 2016)