Difference between revisions of "Cosh"
From specialfunctionswiki
| Line 27: | Line 27: | ||
=References= | =References= | ||
| − | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Sinh|next=Tanh}}: 4.5.2 | + | * {{BookReference|Handbook of mathematical functions|1964|Milton Abramowitz|author2=Irene A. Stegun|prev=Sinh|next=Tanh}}: $4.5.2$ |
{{:Hyperbolic trigonometric functions footer}} | {{:Hyperbolic trigonometric functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 19:37, 22 November 2016
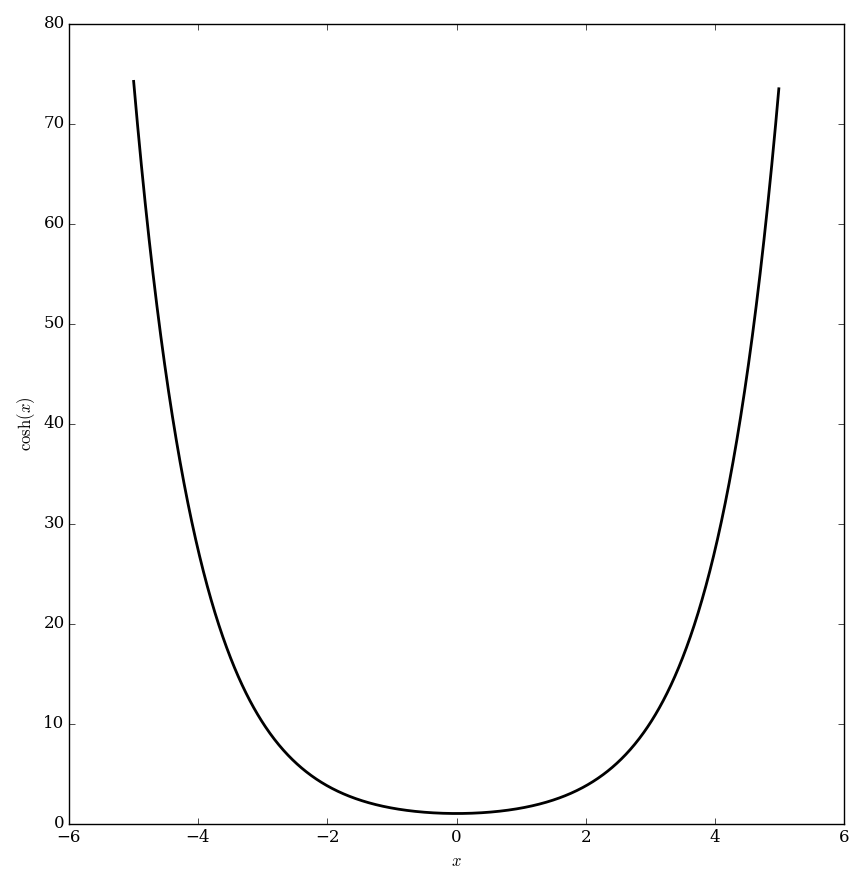
The hyperbolic cosine function $\cosh \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by
$$\mathrm{cosh}(z)=\dfrac{e^z + e^{-z}}{2}$$
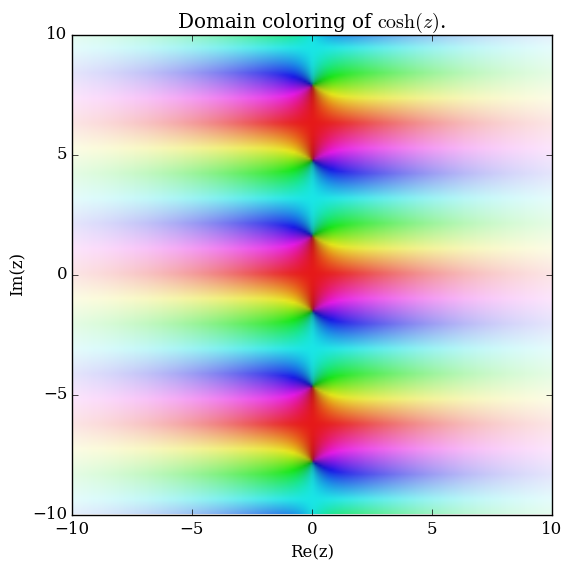
Domain coloring of analytic continuation of $\cosh$.
Properties
Derivative of cosh
Pythagorean identity for sinh and cosh
Weierstrass factorization of cosh
Relationship between cosh and hypergeometric 0F1
Relationship between Bessel I sub 1/2 and cosh
Relationship between cosh and cos
Relationship between cos and cosh
Relationship between secant, Gudermannian, and cosh
Relationship between cosh, inverse Gudermannian, and sec
Period of cosh
See Also
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $4.5.2$