Difference between revisions of "Sine integral"
From specialfunctionswiki
(→Videos) |
|||
| Line 1: | Line 1: | ||
__NOTOC__ | __NOTOC__ | ||
The sine integral is defined by | The sine integral is defined by | ||
| − | $$\mathrm{Si}(z) = \displaystyle\int_0^z \mathrm{sinc}(t) \mathrm{d}t, \quad |\mathrm{arg} z|<\pi,$$ | + | $$\mathrm{Si}(z) = \displaystyle\int_0^z \mathrm{sinc}(t) \mathrm{d}t, \quad |\mathrm{arg} \hspace{2pt} z|<\pi,$$ |
where $\mathrm{sinc}$ denotes the [[sinc]] function. | where $\mathrm{sinc}$ denotes the [[sinc]] function. | ||
Revision as of 19:48, 10 December 2016
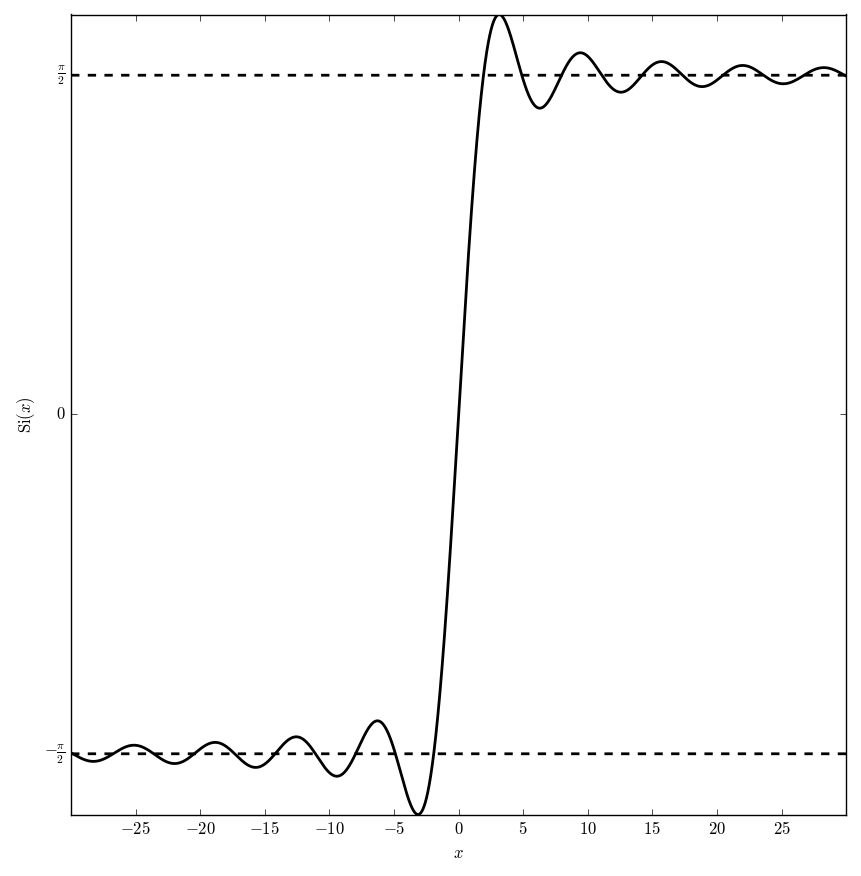
The sine integral is defined by $$\mathrm{Si}(z) = \displaystyle\int_0^z \mathrm{sinc}(t) \mathrm{d}t, \quad |\mathrm{arg} \hspace{2pt} z|<\pi,$$ where $\mathrm{sinc}$ denotes the sinc function.
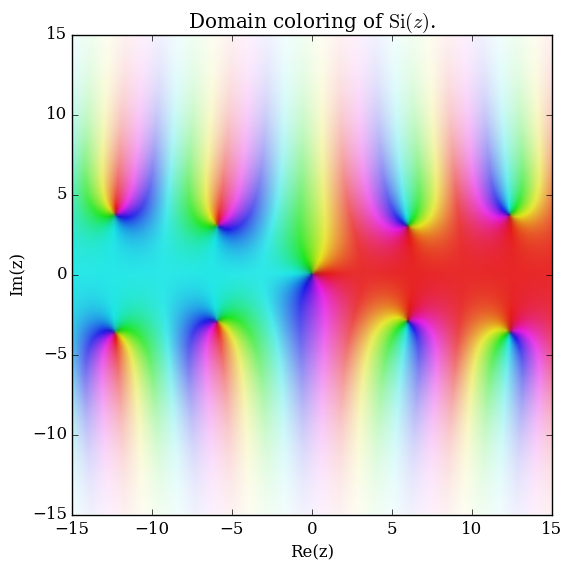
Domain coloring of $\mathrm{Si}$.
Properties
Derivative of sine integral
Antiderivative of sine integral
Relationship between exponential integral Ei, cosine integral, and sine integral
Videos
Laplace Transform of Sine Integral (2 January 2015)
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous): $5.2.1$