Difference between revisions of "Devil's staircase"
From specialfunctionswiki
| Line 1: | Line 1: | ||
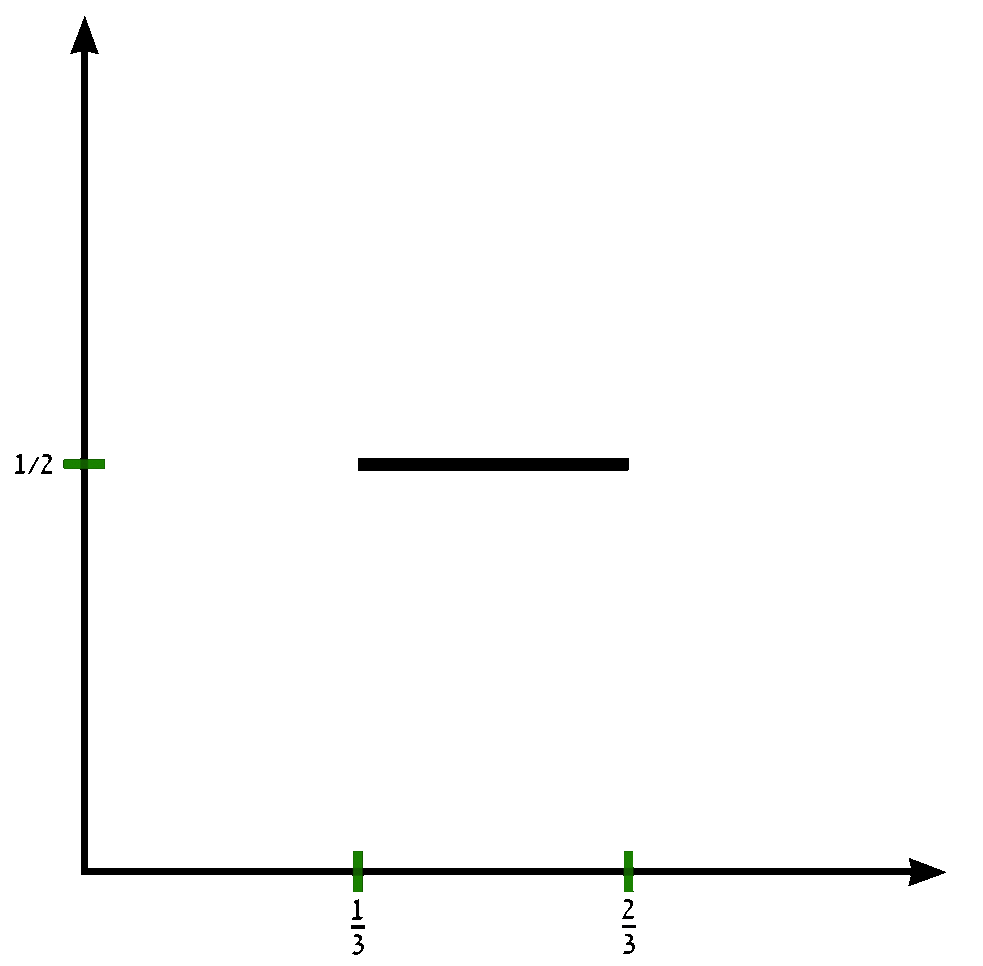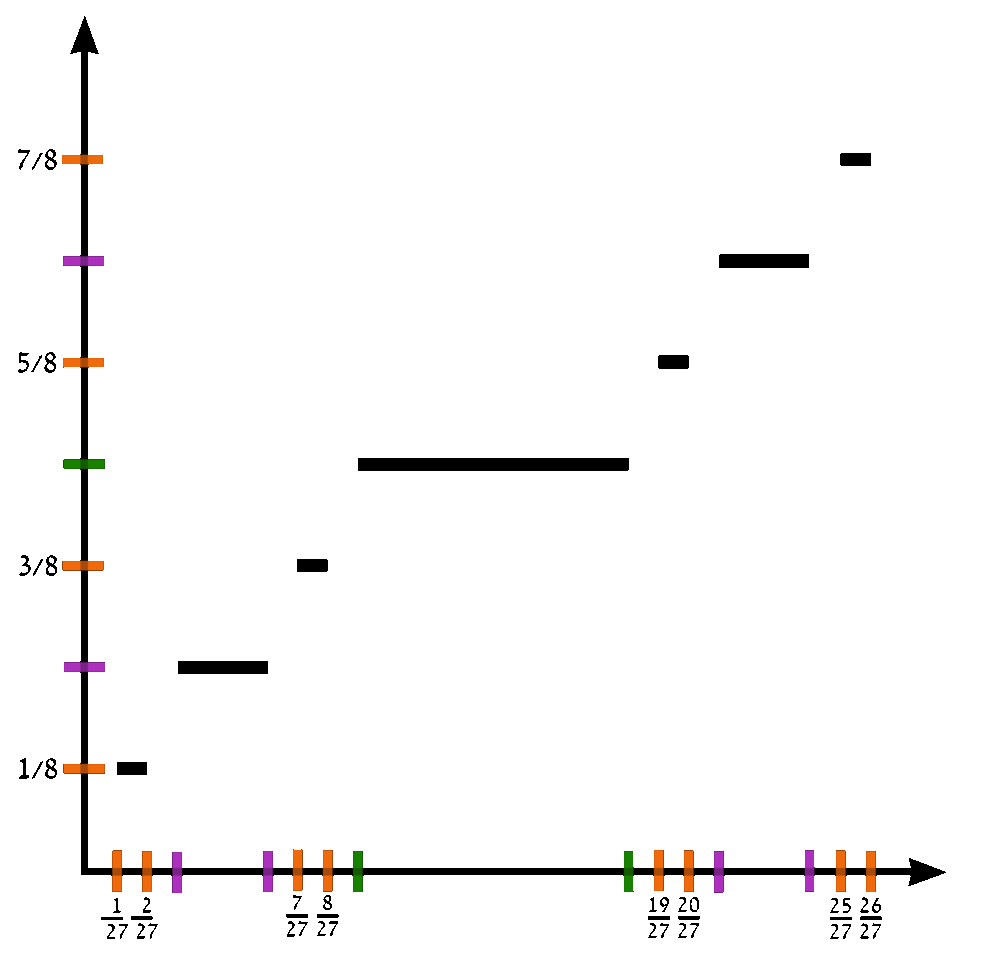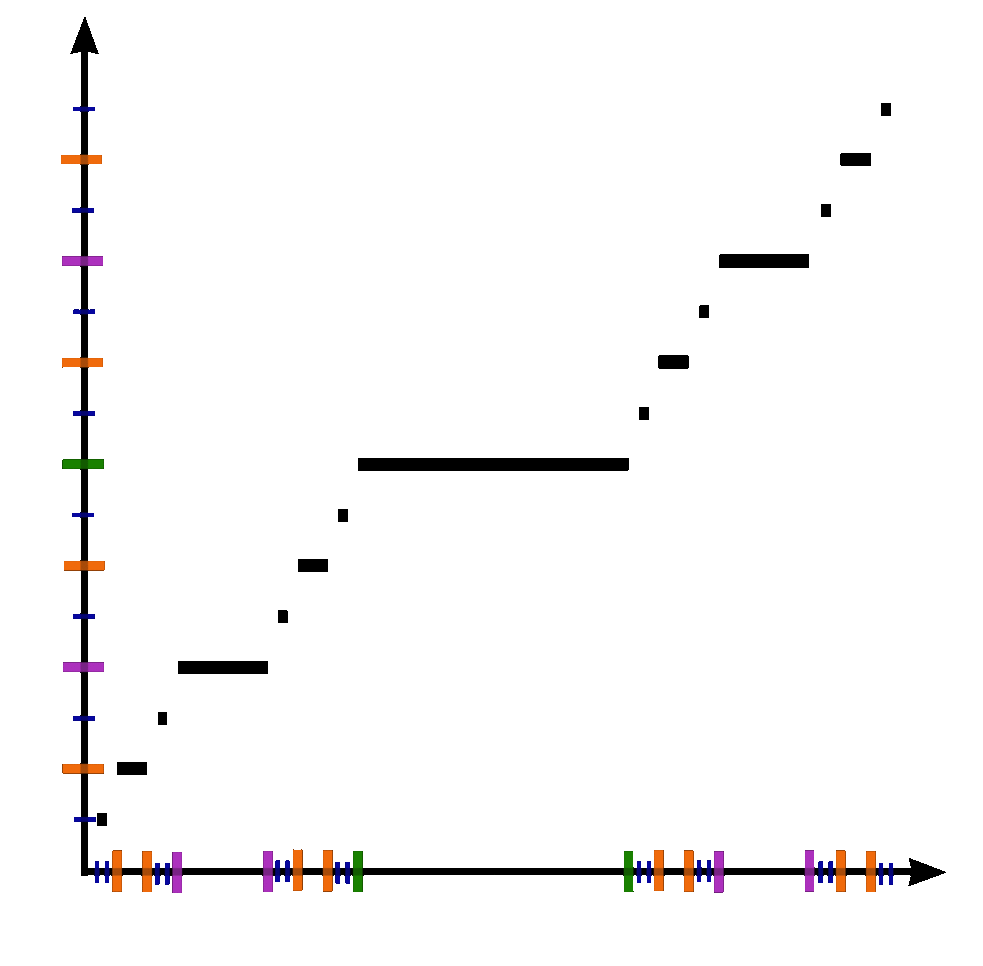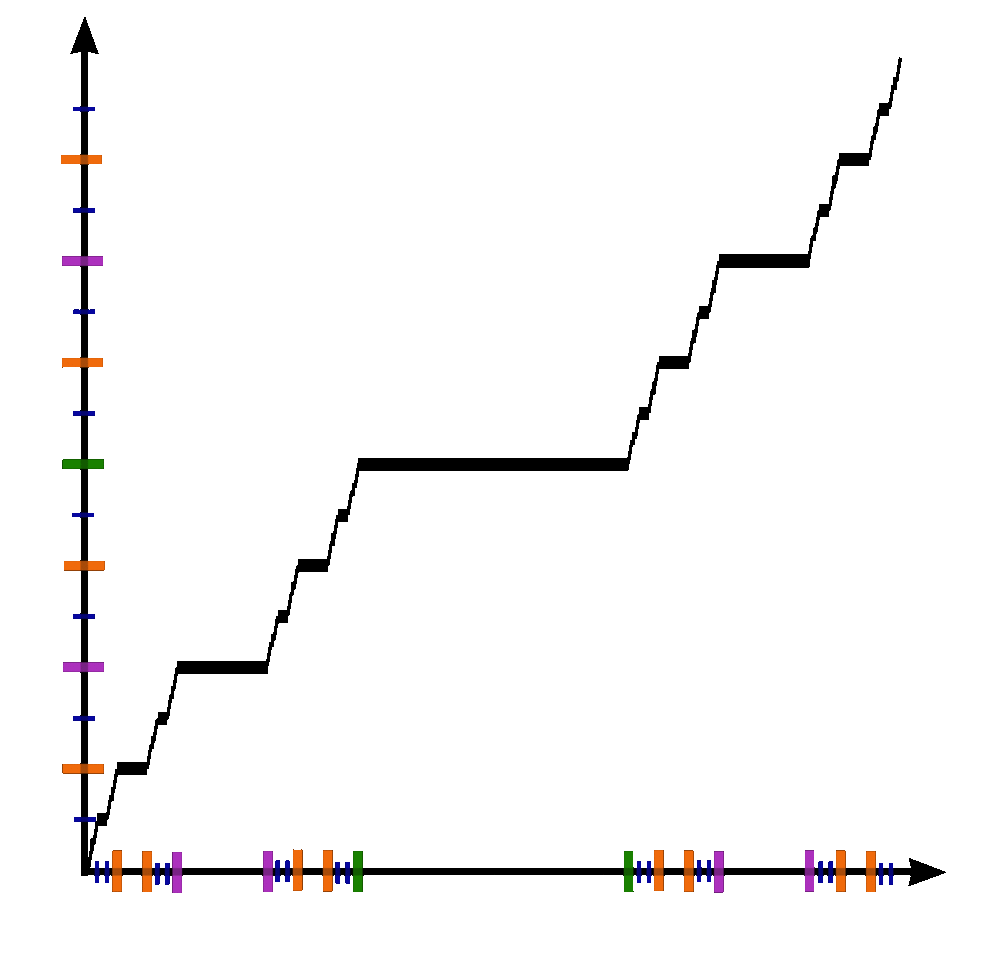
| − | The Devil's staircase | + | The Devil's staircase (also known as the Cantor function) is a function $c \colon [0,1] \rightarrow [0,1]$ can be expressed by the following rules: |
# Write $x$ in base-3. | # Write $x$ in base-3. | ||
# If that representation of $x$ contains a $1$, replace every digit after the first $1$ with $0$'s. | # If that representation of $x$ contains a $1$, replace every digit after the first $1$ with $0$'s. | ||
Revision as of 00:08, 11 December 2016
The Devil's staircase (also known as the Cantor function) is a function $c \colon [0,1] \rightarrow [0,1]$ can be expressed by the following rules:
- Write $x$ in base-3.
- If that representation of $x$ contains a $1$, replace every digit after the first $1$ with $0$'s.
- Replace all $2$'s with $1$'s.
- The resulting expansion defines $c(x)$.