Difference between revisions of "Bessel-Clifford"
From specialfunctionswiki
| Line 2: | Line 2: | ||
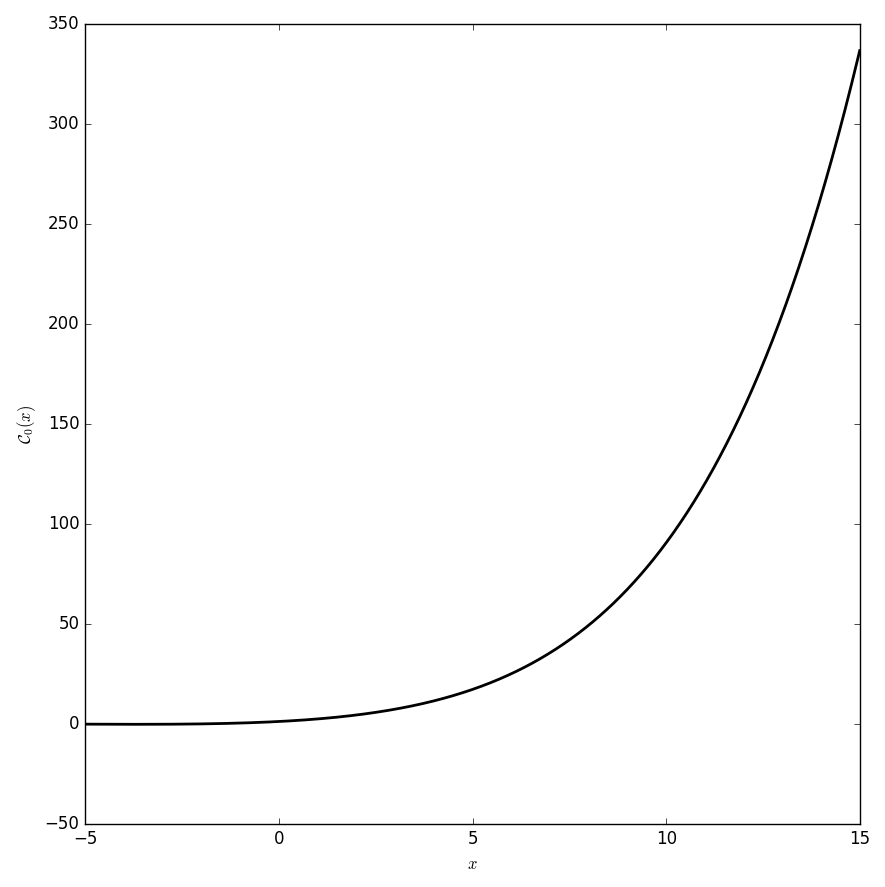
$$\mathcal{C}_n(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{1}{\Gamma(k+n+1)} \dfrac{z^k}{k!},$$ | $$\mathcal{C}_n(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{1}{\Gamma(k+n+1)} \dfrac{z^k}{k!},$$ | ||
where $\dfrac{1}{\Gamma}$ denotes the [[reciprocal gamma]] function. | where $\dfrac{1}{\Gamma}$ denotes the [[reciprocal gamma]] function. | ||
| + | |||
| + | <div align="center"> | ||
| + | <gallery> | ||
| + | File:Besselcliffordn=0plot.png|Graph of $\mathcal{C}_0$ on $[-1,1]$. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | |||
=Properties= | =Properties= | ||
Revision as of 16:03, 29 April 2017
The Bessel-Clifford function $\mathcal{C}_n$ is defined by $$\mathcal{C}_n(z)=\displaystyle\sum_{k=0}^{\infty} \dfrac{1}{\Gamma(k+n+1)} \dfrac{z^k}{k!},$$ where $\dfrac{1}{\Gamma}$ denotes the reciprocal gamma function.
Graph of $\mathcal{C}_0$ on $[-1,1]$.
Properties
Derivative of Bessel-Clifford
Bessel J in terms of Bessel-Clifford
Relationship between Bessel-Clifford and hypergeometric 0F1
