Difference between revisions of "Cosine integral"
From specialfunctionswiki
(→Videos) |
|||
| Line 19: | Line 19: | ||
=References= | =References= | ||
| − | * | + | * {{BookReference|Special Functions of Mathematical Physics and Chemistry|1956|Ian N. Sneddon|prev=findme|next=Sine integral}}: $\S 5 (5.10)$ |
{{:*-integral functions footer}} | {{:*-integral functions footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 00:41, 25 June 2017
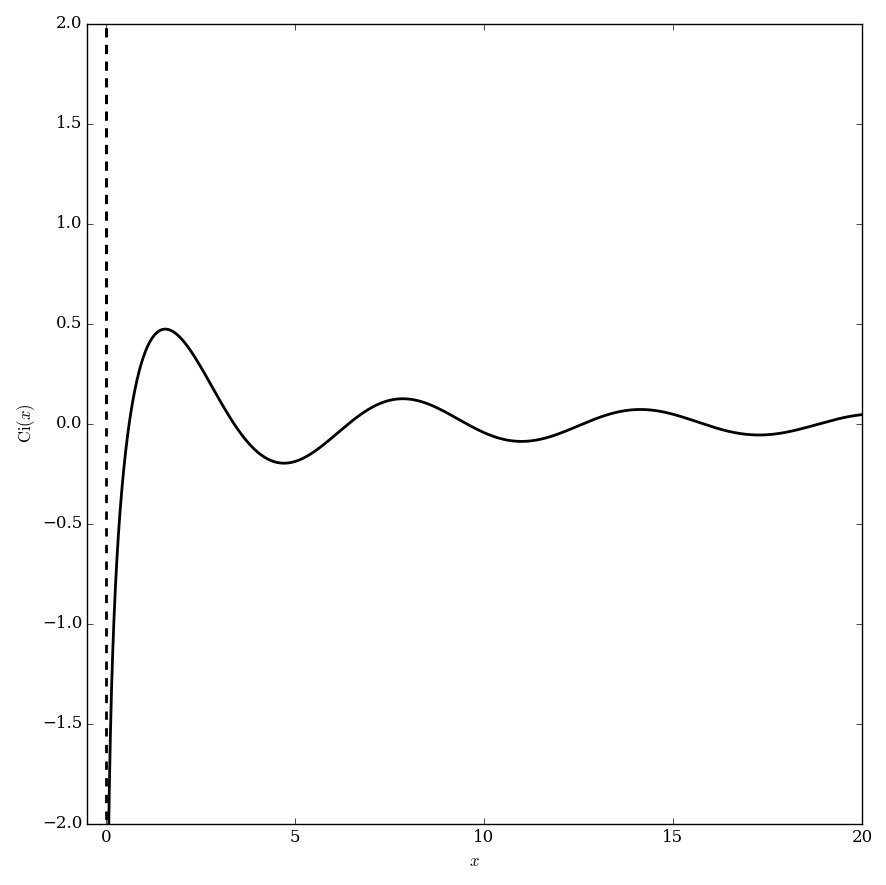
The cosine integral is defined by $$\mathrm{Ci}(z) = -\displaystyle\int_z^{\infty} \dfrac{\cos t}{t} \mathrm{d}t, \quad |\mathrm{arg} z|<\pi.$$
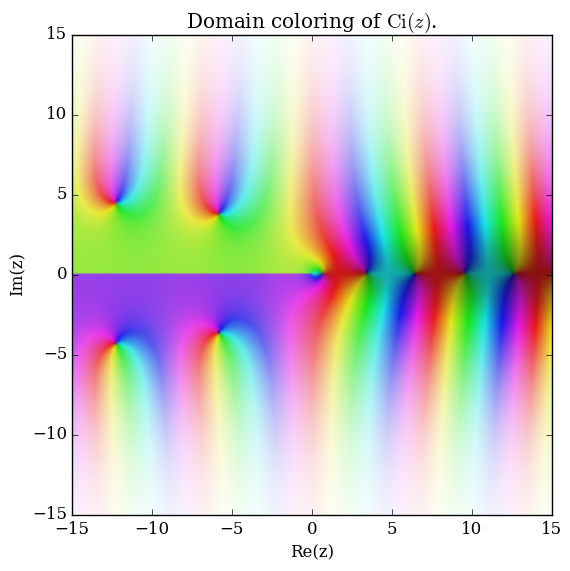
Domain coloring of $\mathrm{Ci}$.
Relationship to other functions
Derivative of cosine integral
Antiderivative of cosine integral
Relationship between exponential integral Ei, cosine integral, and sine integral
Videos
Laplace transform of cosine integral (2 January 2015)
References
- 1956: Ian N. Sneddon: Special Functions of Mathematical Physics and Chemistry ... (previous) ... (next): $\S 5 (5.10)$