Difference between revisions of "Signum"
From specialfunctionswiki
| Line 5: | Line 5: | ||
-1, & x < 0 | -1, & x < 0 | ||
\end{array} \right.$$ | \end{array} \right.$$ | ||
| + | The function is occasionally extended to a function $\mathrm{sgn} \colon \mathbb{C} \rightarrow \mathbb{C}$ by | ||
| + | $$\mathrm{sgn}(z)=\dfrac{z}{|z|}.$$ | ||
<div align="center"> | <div align="center"> | ||
| Line 19: | Line 21: | ||
=References= | =References= | ||
| − | * {{BookReference|Orthogonal Polynomials|1975|Gabor Szegő|edpage = Fourth Edition|prev= | + | * {{BookReference|Orthogonal Polynomials|1975|Gabor Szegő|edpage = Fourth Edition|next=Signum}}: $(1.1.1)$ |
| + | * {{BookReference|Orthogonal Polynomials|1975|Gabor Szegő|edpage = Fourth Edition|prev=Signum|next=findme}}: $(1.1.2)$ | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Latest revision as of 05:12, 11 February 2018
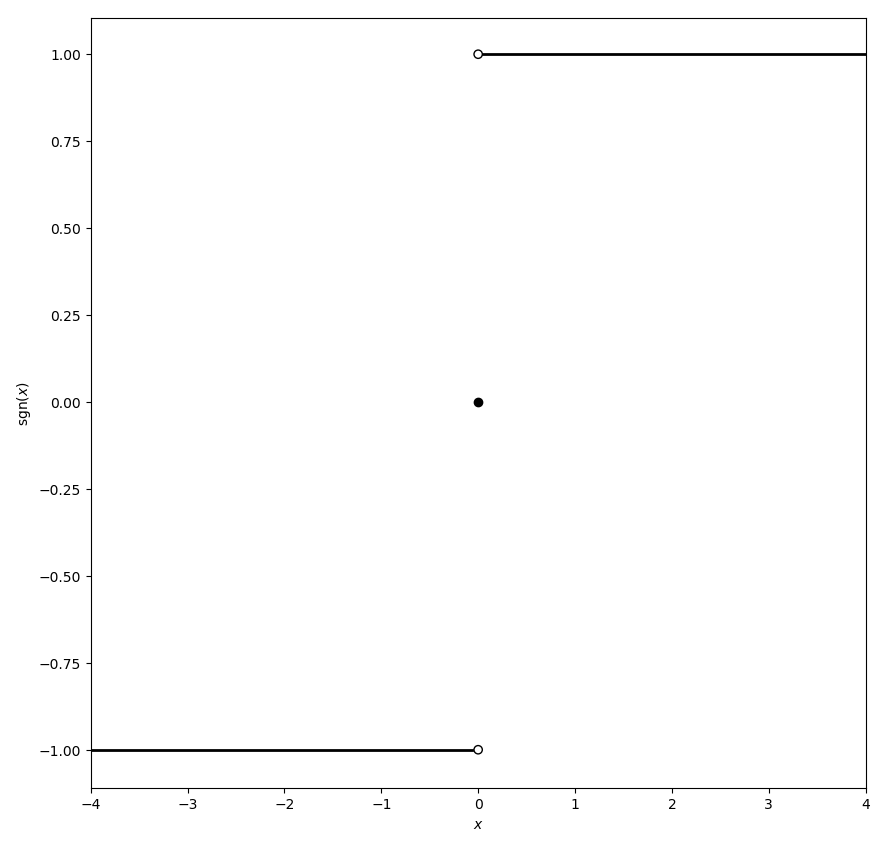
The signum function $\mathrm{sgn} \colon \mathbb{R} \rightarrow \{-1,0,1\}$ (also called the sign function) is the function $$\mathrm{sgn}(x)=\left\{ \begin{array}{ll} 1, & x > 0 \\ 0, & x = 0 \\ -1, & x < 0 \end{array} \right.$$ The function is occasionally extended to a function $\mathrm{sgn} \colon \mathbb{C} \rightarrow \mathbb{C}$ by $$\mathrm{sgn}(z)=\dfrac{z}{|z|}.$$
Properties
Videos
What is Signum Function in Mathematics - Learn Relations and Functions (28 January 2013)
Signum Function (26 August 2016)
References
- 1975: Gabor Szegő: Orthogonal Polynomials ... (next): $(1.1.1)$
- 1975: Gabor Szegő: Orthogonal Polynomials ... (previous) ... (next): $(1.1.2)$