Difference between revisions of "Laguerre L"
| Line 72: | Line 72: | ||
=References= | =References= | ||
| + | * {{BookReference|Special Functions for Scientists and Engineers|1968|W.W. Bell|prev=findme|next=findme}}: $(6.3)$ | ||
{{:Orthogonal polynomials footer}} | {{:Orthogonal polynomials footer}} | ||
[[Category:SpecialFunction]] | [[Category:SpecialFunction]] | ||
Revision as of 13:45, 15 March 2018
The Laguerre polynomial of order $n$, $L_n$, is given by $$L_n(x) = \displaystyle\sum_{k=0}^n \dfrac{(-1)^kn!}{(n-k)!(k!)^2}x^k.$$
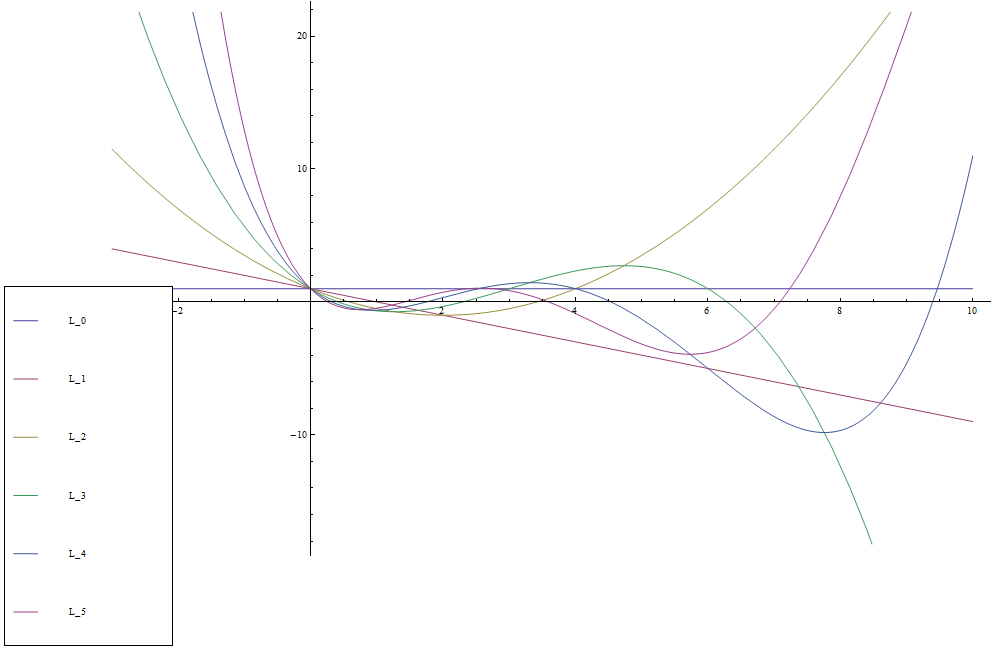
The first few Laguerre polynomials are given by $$\begin{array}{ll} L_0(x) &= 1 \\ L_1(x) &= -x+1 \\ L_2(x) &= \dfrac{1}{2}(x^2-4x+2) \\ L_3(x) &= \dfrac{1}{6}(-x^3+9x^2-18x+6) \\ L_4(x) &= \dfrac{1}{24}(x^4-16x^3+72x^2-96x+24)\\ \vdots \end{array}$$
Graph of $L_n$ for $n=0,1,2,\ldots,5$ on $[-3,10]$.
Properties
Theorem: The following formula holds: $$\dfrac{e^{\frac{-xt}{1-t}}}{1-t} = \displaystyle\sum_{k=0}^{\infty} L_k(x)t^k.$$
Proof: █
Theorem: The following formula holds: $$L_n(x) = \dfrac{e^x}{n!} \dfrac{d^n}{dx^n} (x^n e^{-x}).$$
Proof: █
Theorem (Orthogonality): The following formula holds: $$\displaystyle\int_0^{\infty} e^{-x}L_n(x)L_m(x)dx = \delta_{nm},$$ where $\delta_{mn}=0$ when $m\neq n$ and $\delta_{mn}=1$ when $m=n$.
Proof: █
Theorem: The following formula holds: $$(n+1)L_{n+1}(x)=(2n+1-x)L_n(x)-nL_{n-1}(x).$$
Proof: █
Theorem: The following formula holds: $$xL_n'(x)=nL_n(x)-nL_{n-1}(x).$$
Proof: █
Theorem: The following formula holds: $$L_n'(x)=-\displaystyle\sum_{k=0}^{n-1} L_k(x).$$
Proof: █
See also
References
- 1968: W.W. Bell: Special Functions for Scientists and Engineers ... (previous) ... (next): $(6.3)$
