Cosine integral
From specialfunctionswiki
The cosine integral is defined by $$\mathrm{Ci}(z) = -\displaystyle\int_z^{\infty} \dfrac{\cos t}{t} dt ; |\mathrm{arg} z|<\pi.$$
- Ci.png
Graph of $\mathrm{arccos}$ on $(0,20)$.
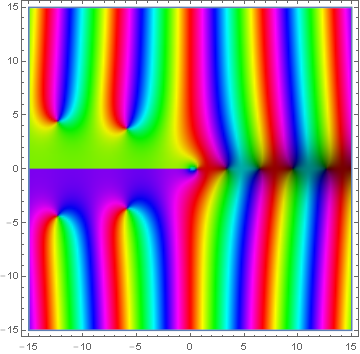
Domain coloring of analytic continuation of $\mathrm{Ci}$.
Contents
Relationship to other functions
Theorem
The following formula holds: $$\mathrm{Ei}(ix)=\mathrm{Ci}(x)+i\mathrm{Si}(x),$$ where $\mathrm{Ei}$ denotes the exponential integral Ei, $\mathrm{Ci}$ denotes the cosine integral, and $\mathrm{Si}$ denotes the sine integral.
Proof
References
Videos
Laplace transform of cosine integral