Riemann function

The Riemann function is the function $R \colon \mathbb{R} \rightarrow \mathbb{R}$ defined by $$R(x)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\sin(k^2 x)}{k^2}.$$

The partial sum $R(x,N)=\displaystyle\sum_{k=1}^N \dfrac{\sin(k^2 x)}{k^2}$ for various values of $N$:

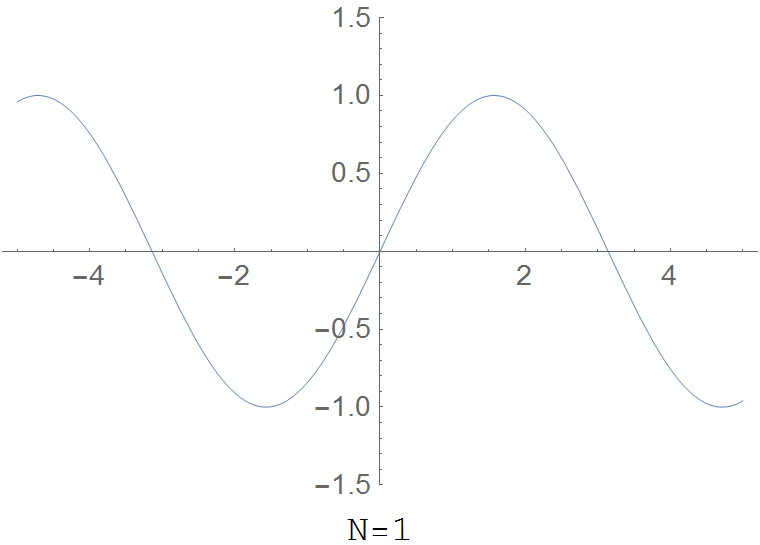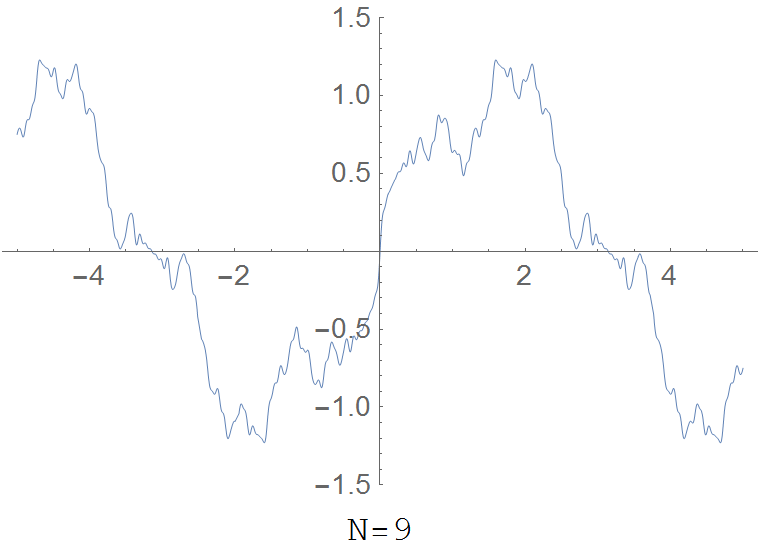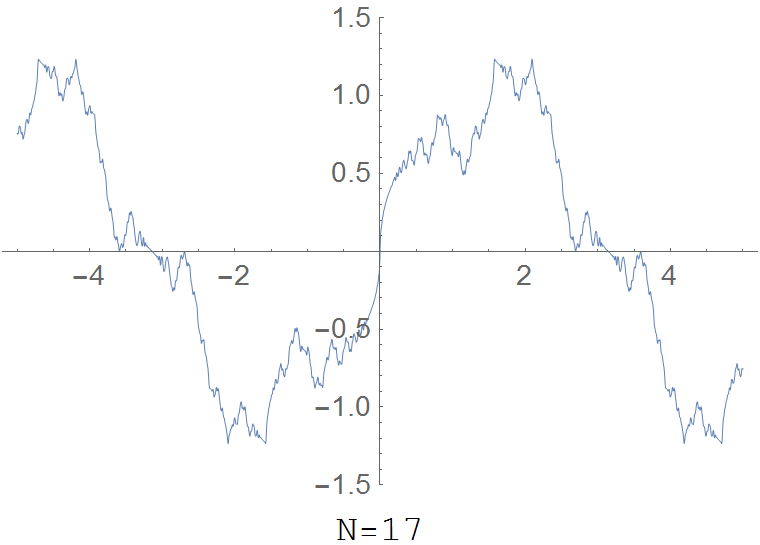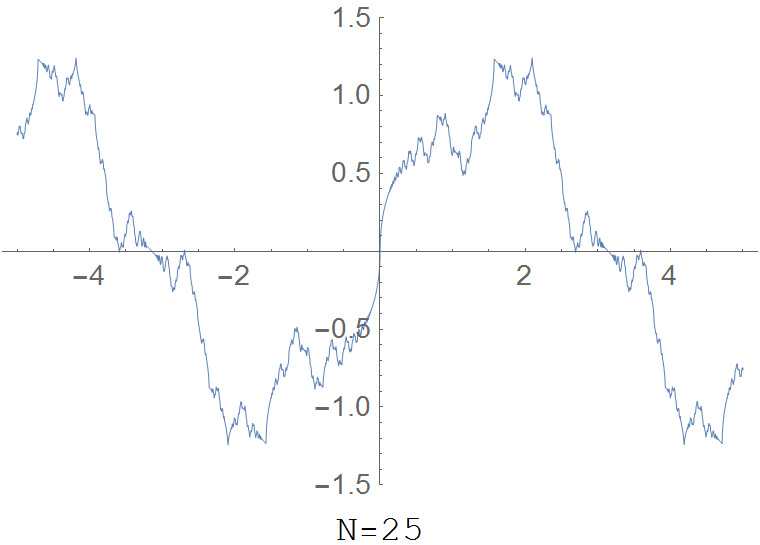
Properties

Theorem: The Riemann function is is continuous.

Proof: █

Theorem: The Riemann function is nowhere differentiable except at points of the form $\pi \dfrac{2p+1}{2q+1}$ with $p,q \in \mathbb{Z}$.

Proof: █

References

[1]