Elliptic E

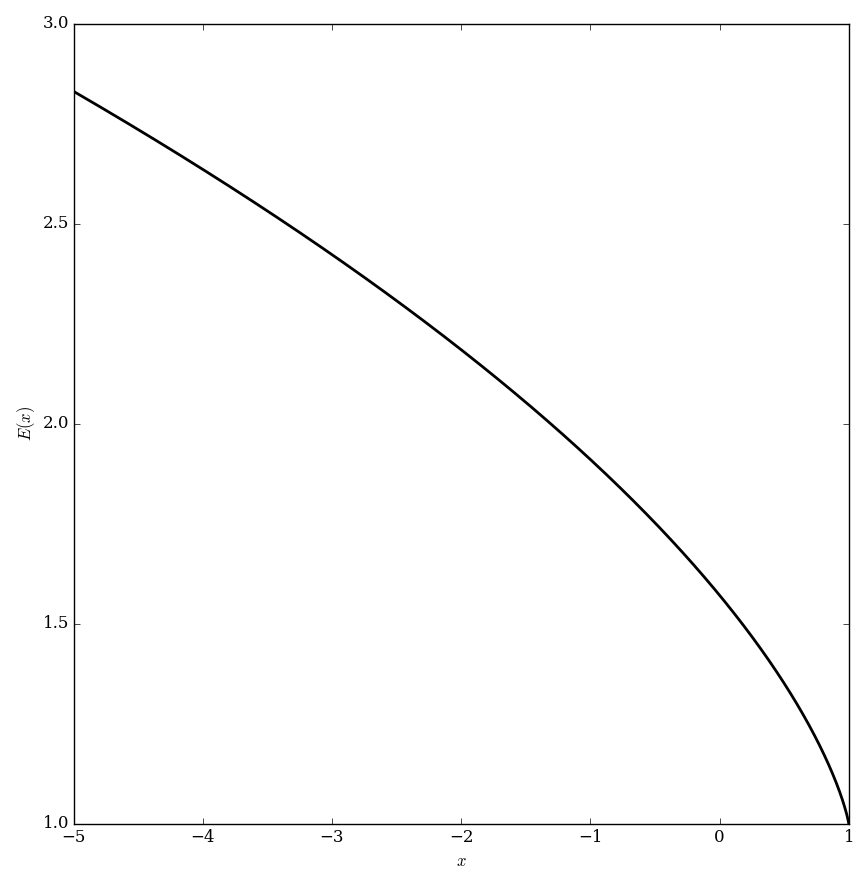
If $m=k^2$ we define the complete elliptic integral of the second kind, $E$, to be $$E(k)=E(m)=\displaystyle\int_0^{\frac{\pi}{2}} \sqrt{1-k^2\sin^2 \theta} \mathrm{d}\theta.$$

• 

  Graph of $E$.

• 

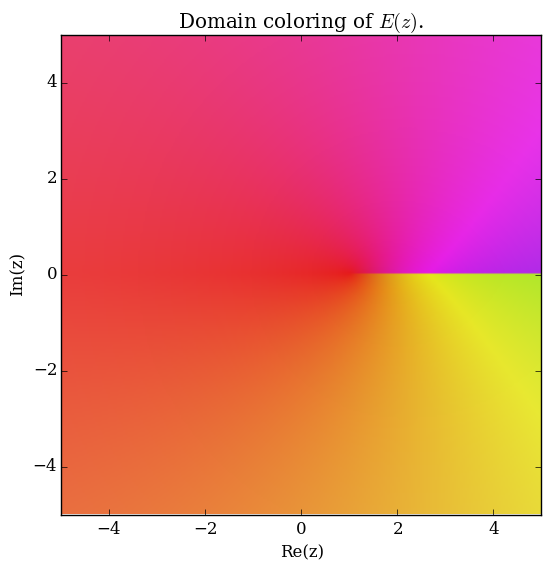
  Domain coloring of $E$.

Properties

E(m)=(pi/2)2F1(-1/2,1/2;1;m)

See Also

Elliptic K
Incomplete Elliptic E

References

"Special Functions" by Leon Hall