Prime counting
From specialfunctionswiki
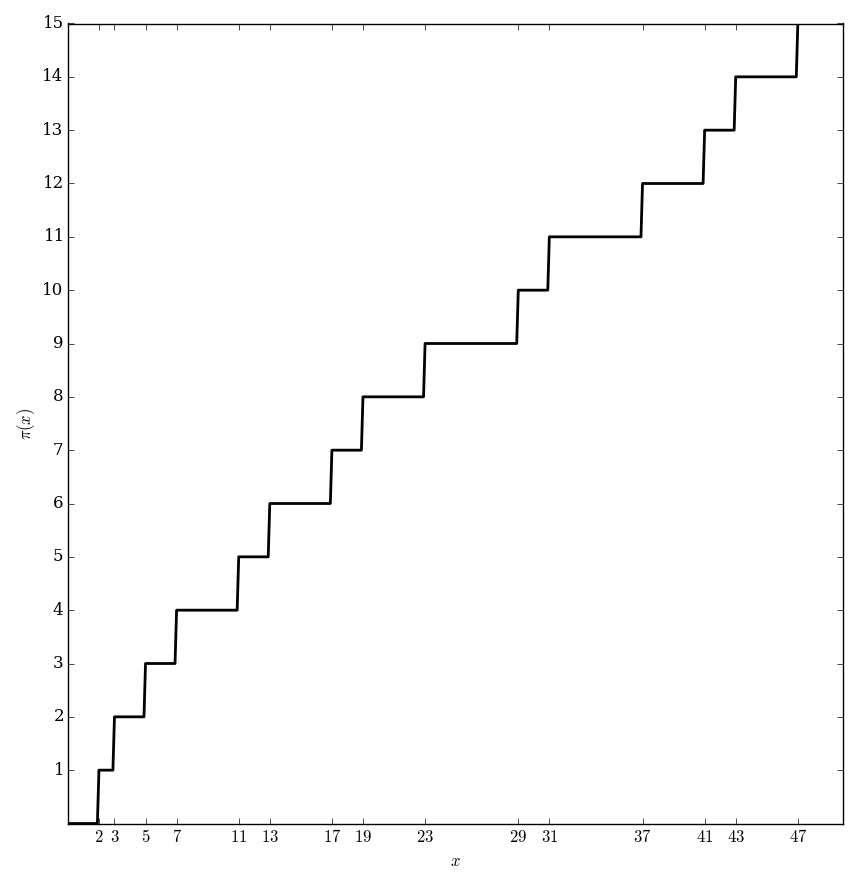
The prime counting function $\pi \colon \mathbb{R} \rightarrow \mathbb{Z}^+$ is defined by the formula $$\pi(x) = \{\mathrm{number \hspace{2pt} of \hspace{2pt} primes} \leq x \}.$$
Properties
Prime number theorem, pi and x/log(x)
Prime number theorem, logarithmic integral
References
Newman's short proof of the prime number theorem