Bessel Y

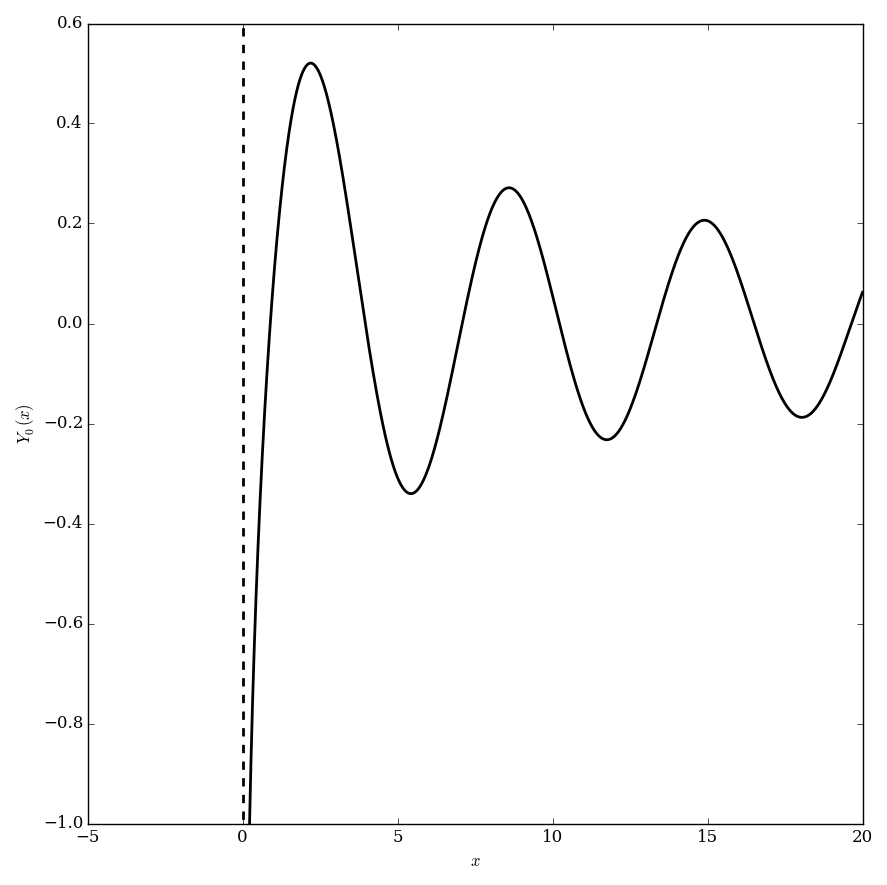
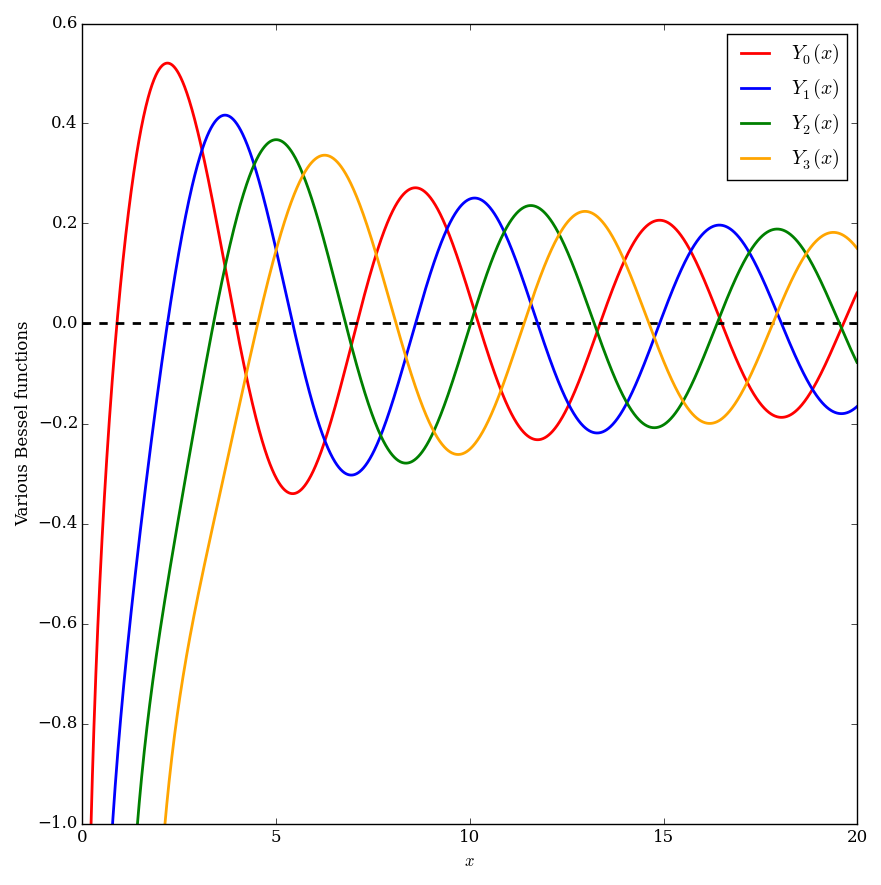
Bessel functions of the second kind, $Y_{\nu}$, are defined via the formula $$Y_{\nu}(z)=\dfrac{J_{\nu}(z)\cos(\nu \pi)-J_{-\nu}(z)}{\sin(\nu \pi)}.$$ Sometimes these functions are called Neumann functions and have the notation $N_{\nu}$ instead of $Y_{\nu}$.

• 

  Graph of $Y_0$.

• 

  Graph of $Y_0,Y_1,Y_2$, and $Y_3$.

• 

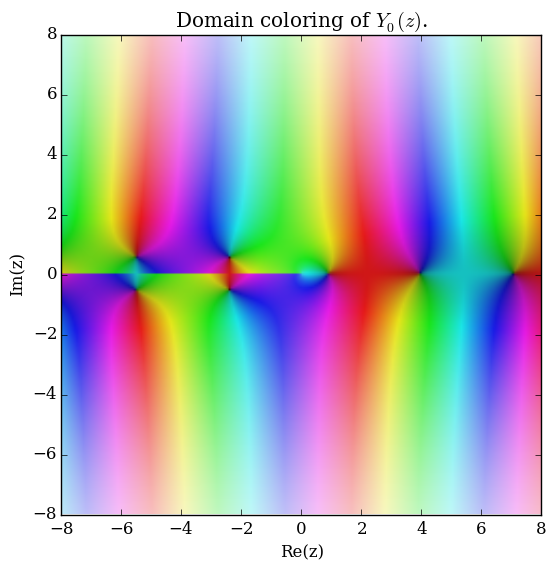
  Domain coloring of $Y_0$.

• 

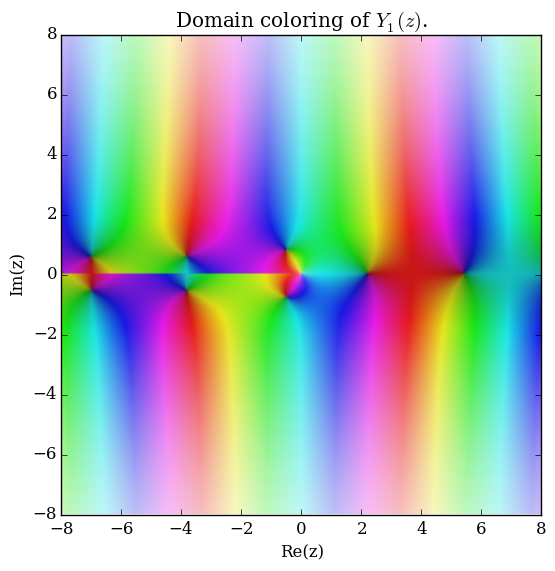
  Domain coloring of $Y_1$.

• 

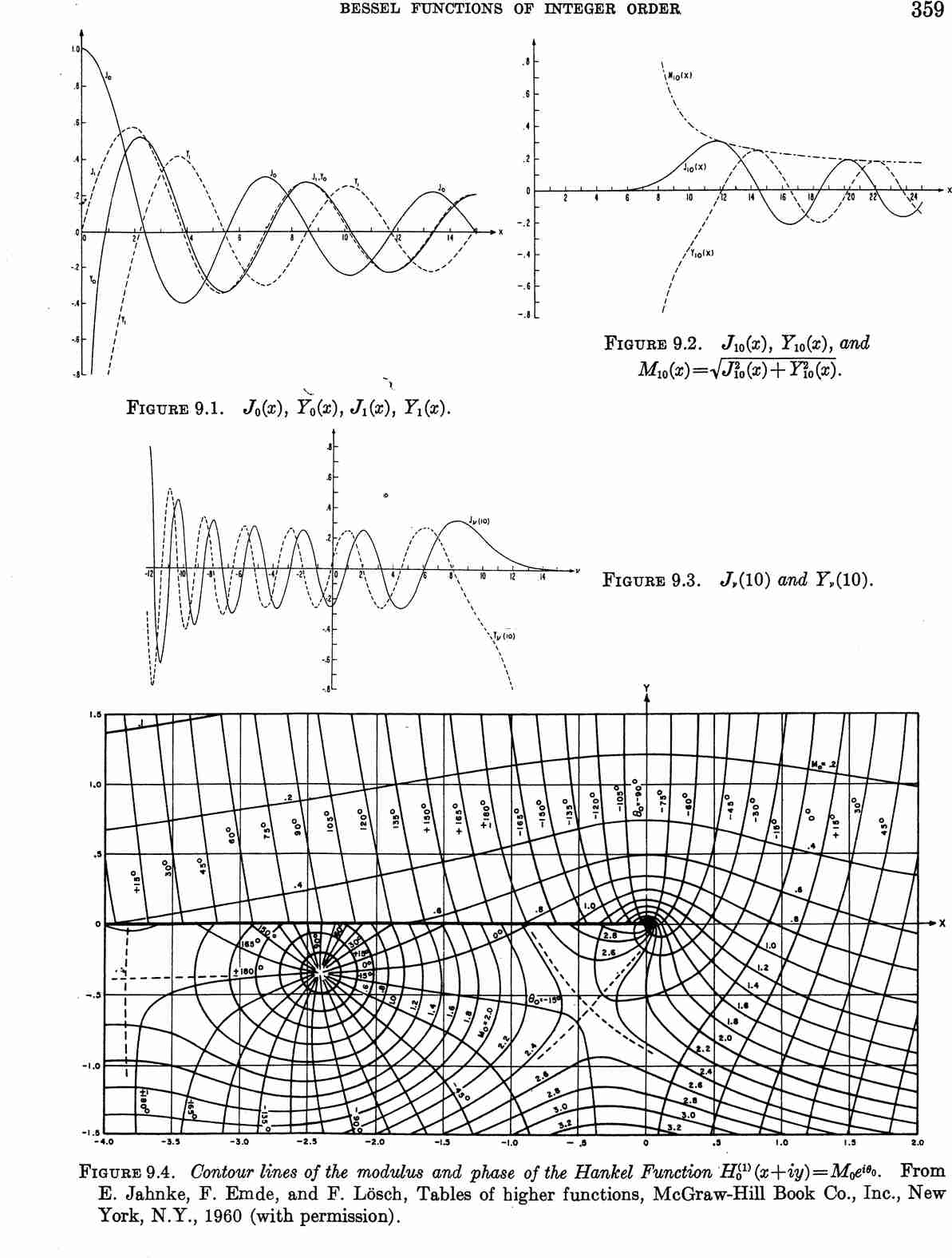
  Bessel functions from Abramowitz&Stegun

Properties

Derivative of Bessel Y with respect to its order

References

• 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 9.1.2

Bessel's functions of the second order - C.V. Coates

Bessel functions

Anger function

Bessel-Clifford

Bessel $J_{\nu}$

Bessel $Y_{\nu}$

Bessel $I_{\nu}$

Modified Bessel $K_{\nu}$

Spherical Bessel $j_{\nu}$

Spherical Bessel $y_{\nu}$