Arccos
From specialfunctionswiki
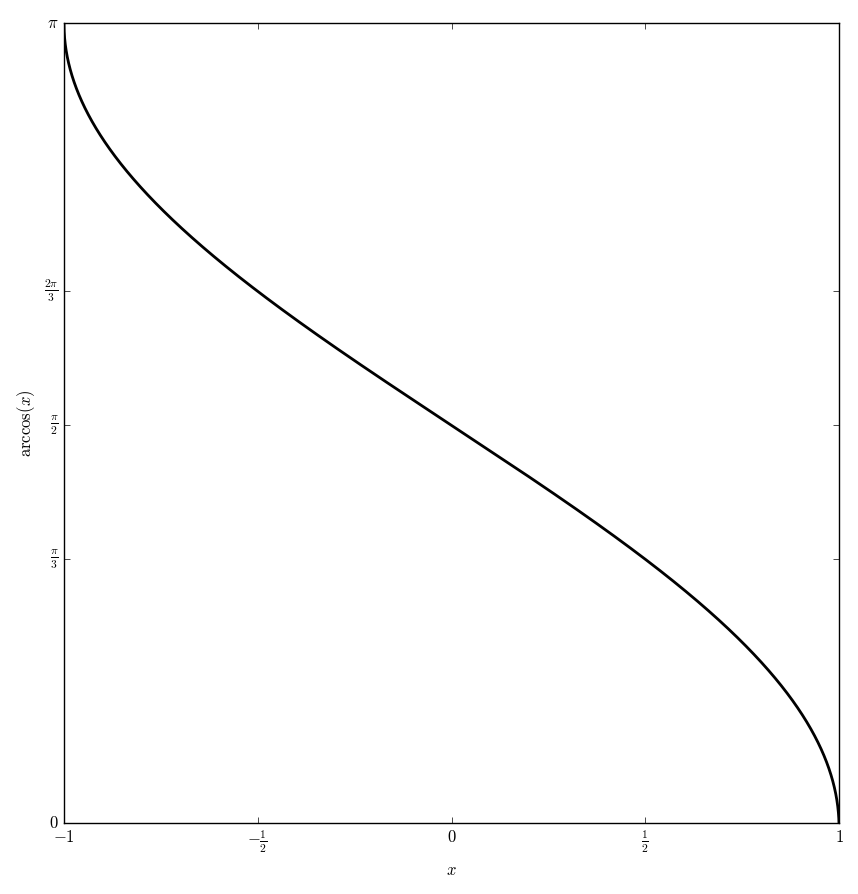
The function $\mathrm{arccos} \colon \mathbb{C} \setminus \{(-\infty,-1) \bigcup (1,\infty) \} \rightarrow \mathbb{C}$ is defined by $$\rm{arccos}(z)=\dfrac{\pi}{2} + i\log\left( iz + \sqrt{1-z^2} \right),$$ where $i$ denotes the imaginary number and $\log$ denotes the logarithm.
Graph of $\mathrm{arccos}$ on $[-1,1]$.
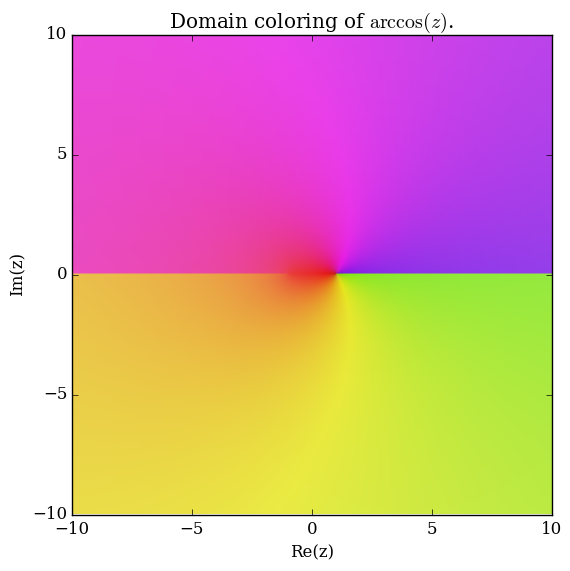
Domain coloring of $\mathrm{arccos}$.
Properties
Derivative of arccos
Antiderivative of arccos
