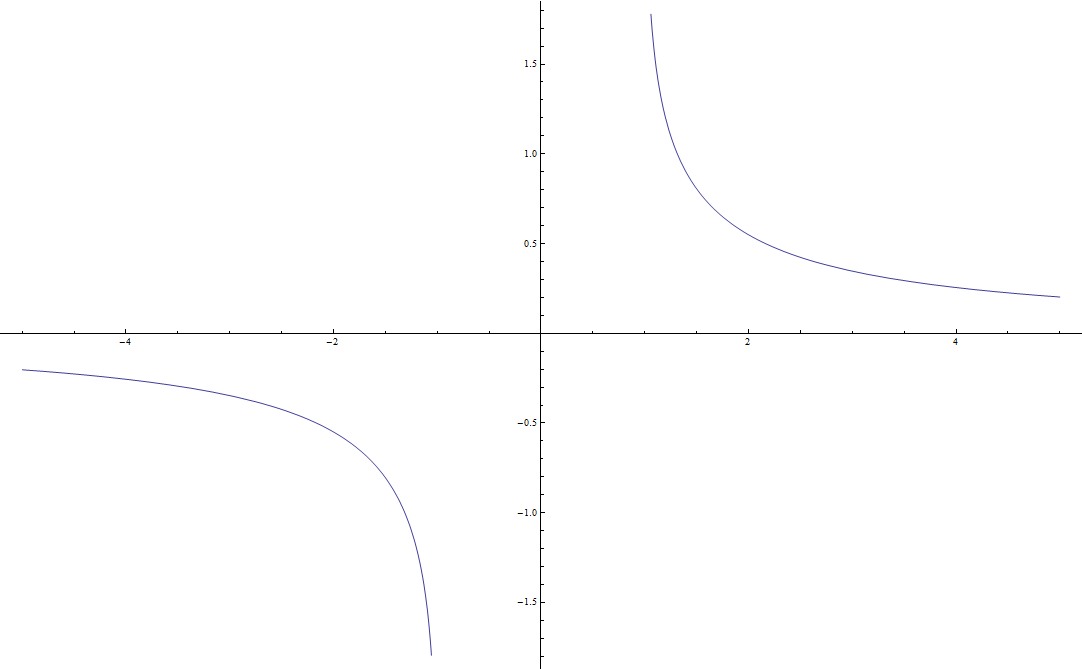
Arccoth
From specialfunctionswiki
The inverse hyperbolic cotangent $\mathrm{arccoth}$ is the inverse function of the hyperbolic cotangent function. It may be defined by the following formula: $$\mathrm{arccoth}(z)=\mathrm{arctanh} \left( \dfrac{1}{z} \right),$$ where $\mathrm{arctanh}$ denotes the inverse hyperbolic tangent.
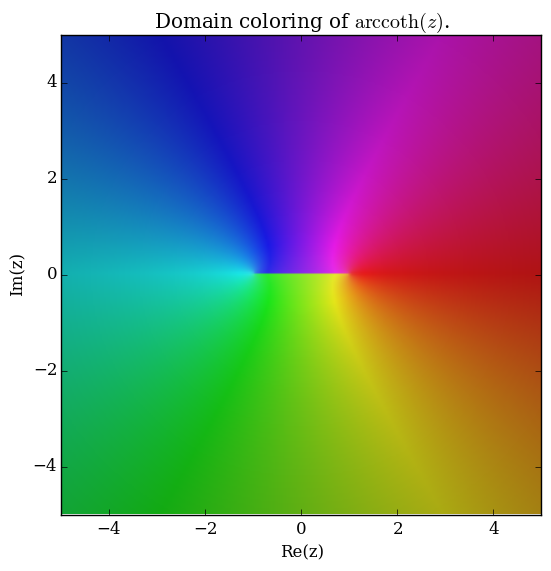
Domain coloring of $\mathrm{arccoth}$.