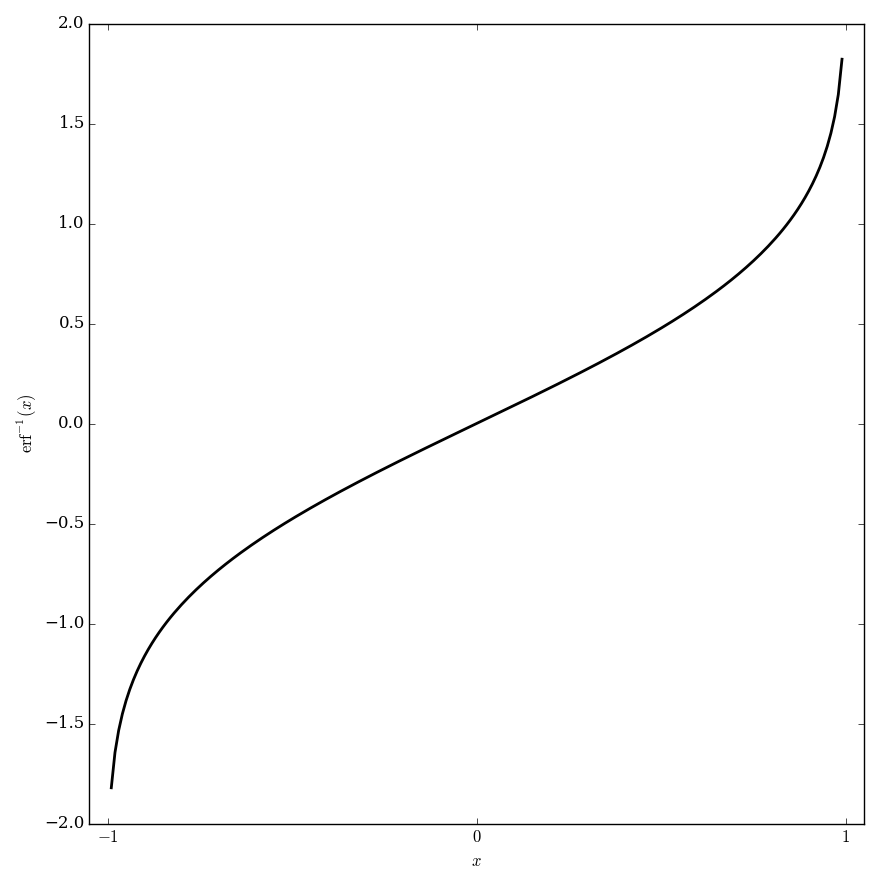
Inverse error function
From specialfunctionswiki
The inverse error function is the inverse function of the error function. We denote it by writing $\mathrm{erf}^{-1}$.
Graph of $\mathrm{erf}^{-1}$.
Properties
Derivative of inverse error function Antiderivative of inverse error function
Theorem: The following formula holds: $$\displaystyle\int_0^1 \mathrm{erf}^{-1}(x) dx=\dfrac{1}{\sqrt{\pi}}.$$
Proof: █
Theorem: The following formula holds: $$\displaystyle\int_0^1 \log(\mathrm{erf}^{-1}(x)) dx = \left( \dfrac{\gamma}{2} + \log(2) \right),$$ where $\mathrm{erf}^{-1}$ denotes the inverse error function, $\log$ denotes the logarithm, and $\gamma$ denotes the Euler-Mascheroni constant.
Proof: █
