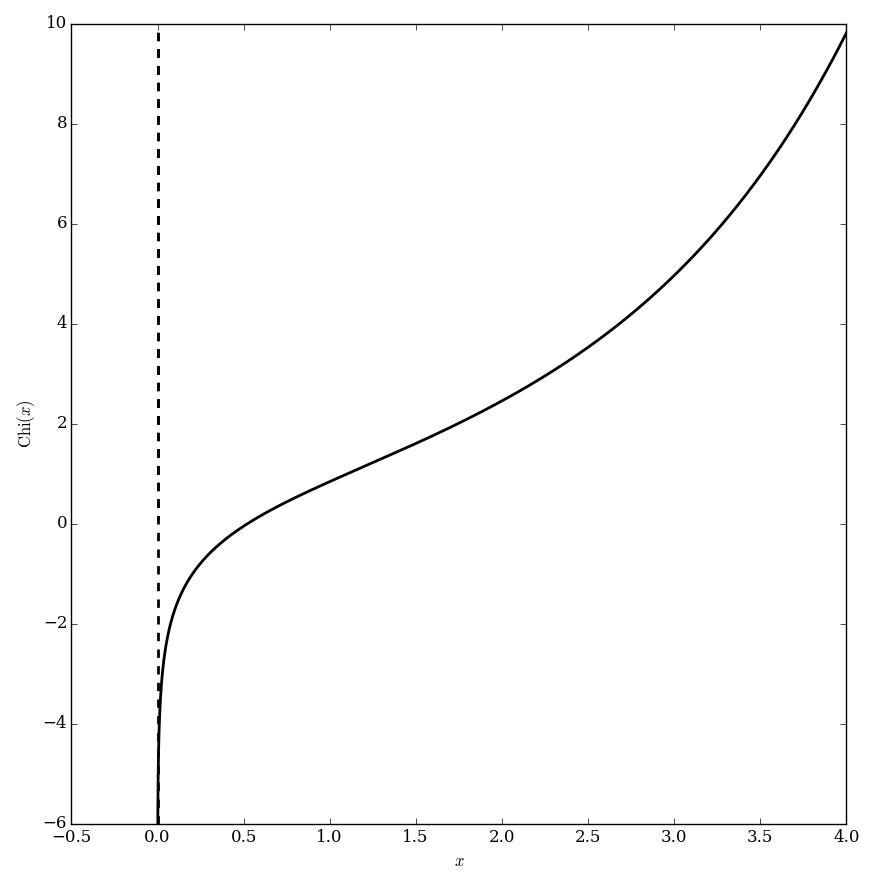
Chi
From specialfunctionswiki
The hyperbolic cosine integral $\mathrm{Chi}$ is defined for $|\mathrm{arg}(z)| < \pi$ the formula $$\mathrm{Chi}(z)=\gamma + \log(z) + \displaystyle\int_0^z \dfrac{\cosh(t)-1}{t} \mathrm{d}t,$$ where $\gamma$ denotes the Euler-Mascheroni constant, $\log$ denotes the logarithm, and $\cosh$ denotes the hyperbolic cosine.
Graph of $\mathrm{Chi}$.
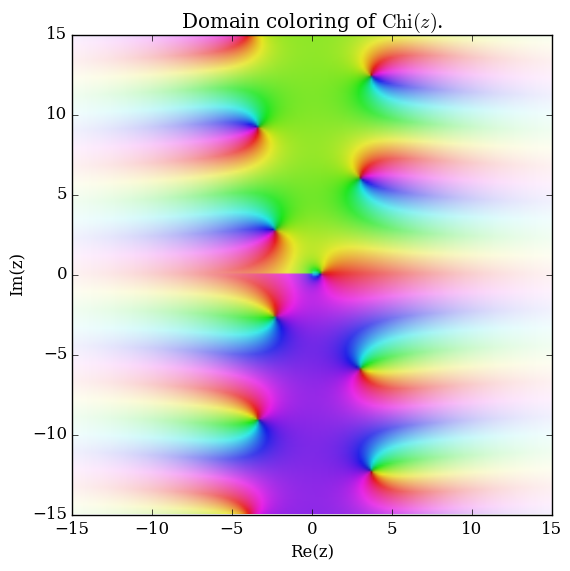
Domain coloring of $\mathrm{Chi}$.
Properties
Derivative of chi
Antiderivative of chi
