Dirichlet beta
From specialfunctionswiki
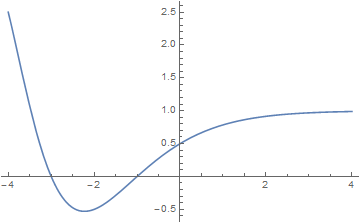
The Dirichlet $\beta$ function is defined by $$\beta(z) = \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k}{(2k+1)^z}.$$
Graph of $\beta$ on $[-4,4]$.
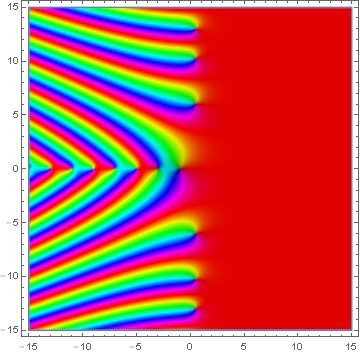
Domain coloring of analytic continuation of $\beta$.
Properties
Catalan's constant using Dirichlet beta
Dirichlet beta in terms of Lerch transcendent
