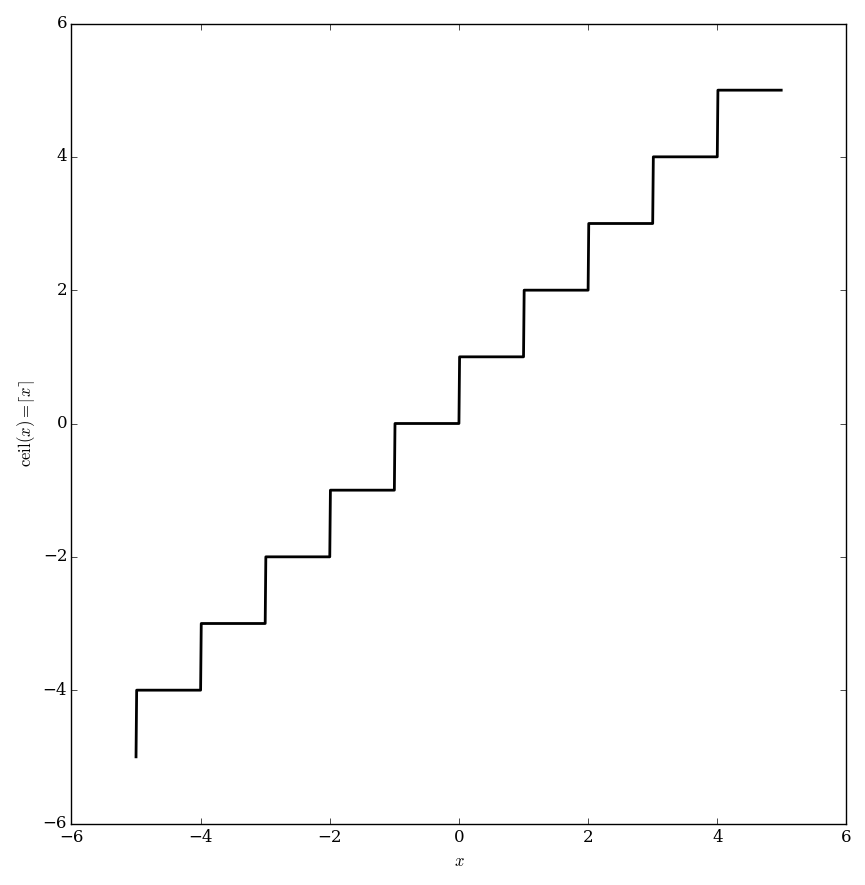
Ceiling
From specialfunctionswiki
The ceiling function $\mathrm{ceil} \colon \mathbb{R} \rightarrow \mathbb{Z}$ (sometimes written $\lceil x \rceil$) is defined by $$\mathrm{ceil}(x) \equiv \lceil x \rceil = \min \{ y \in \mathbb{Z} \colon y \geq x \},$$ i.e., the smallest integer greater than or equal to $x$.