Devil's staircase

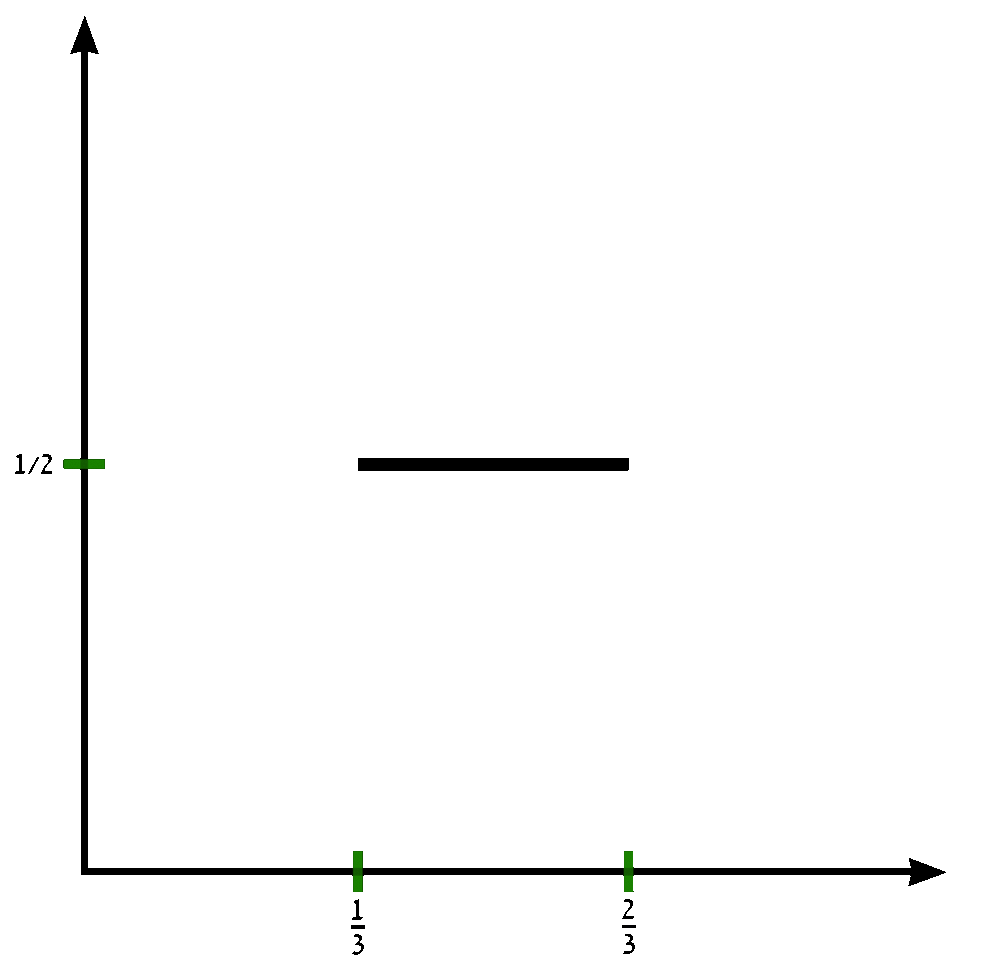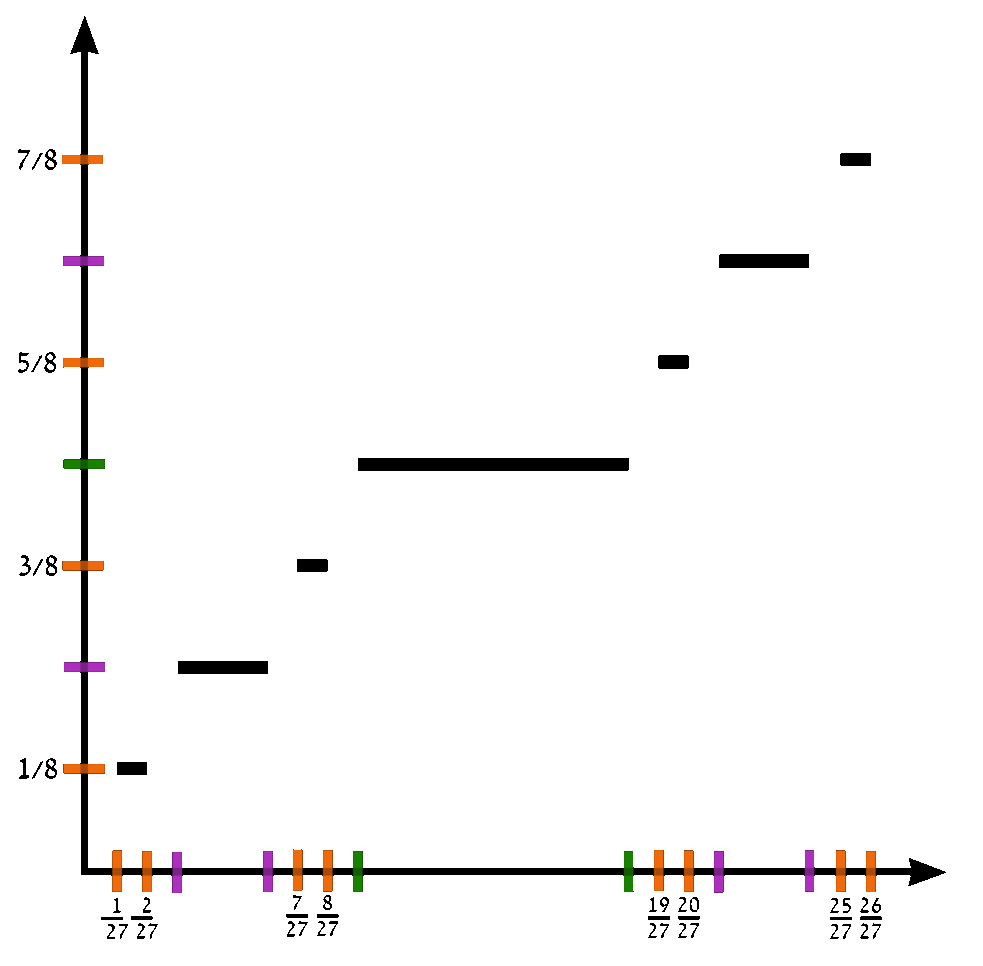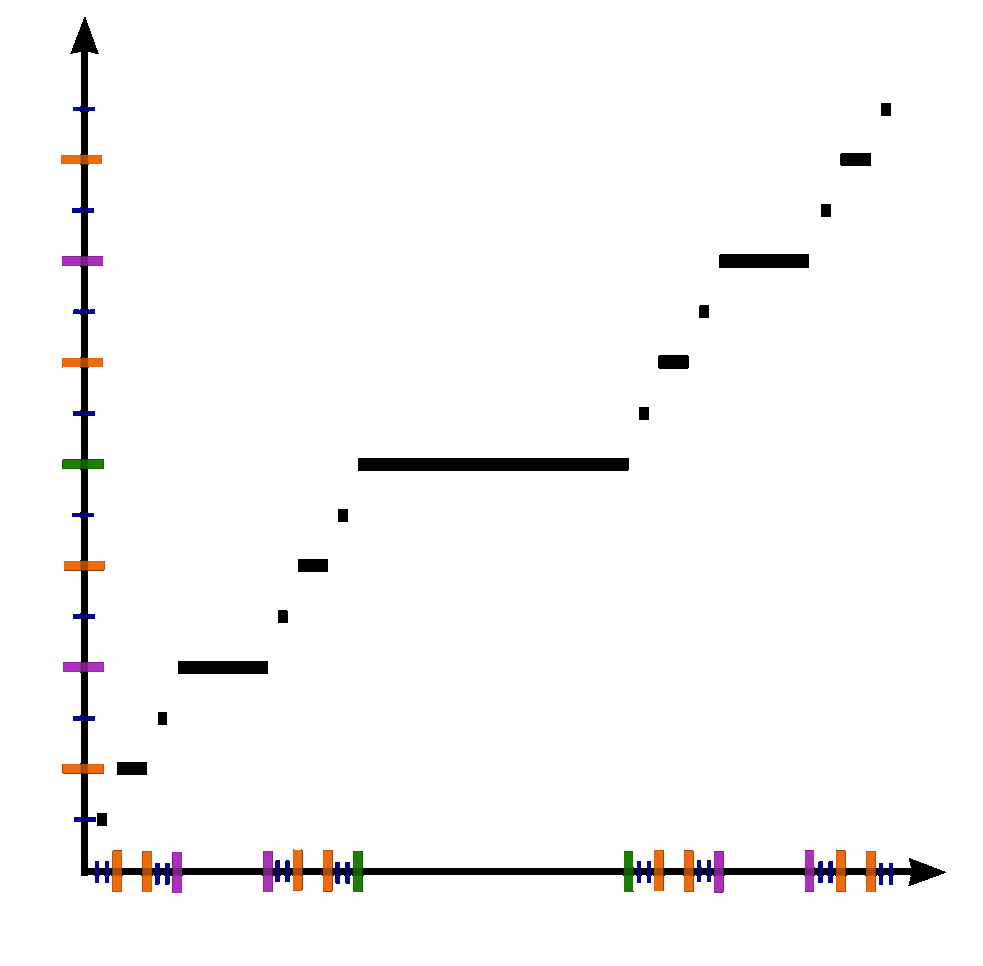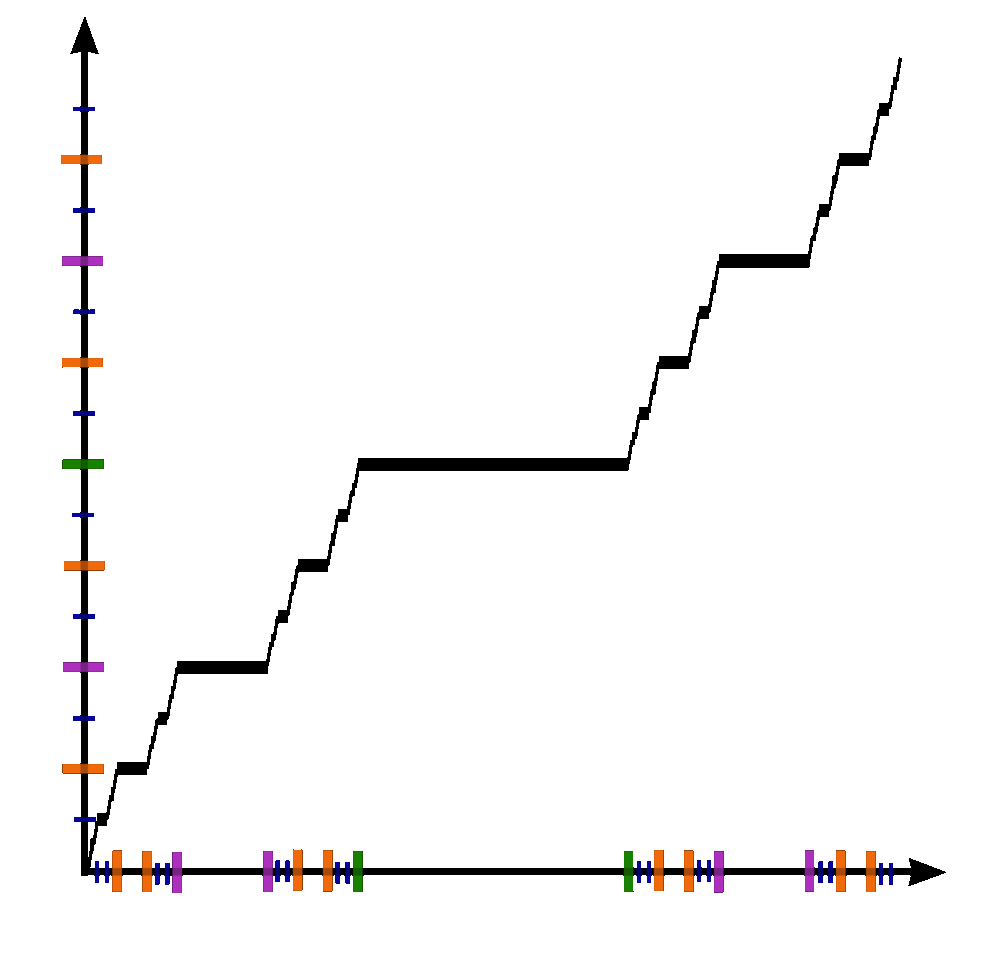
The Devil's staircase (also known as the Cantor function) is a function $c \colon [0,1] \rightarrow [0,1]$ can be expressed by the following rules:

1. Write $x$ in base-3.
2. If that representation of $x$ contains a $1$, replace every digit after the first $1$ with $0$'s.
3. Replace all $2$'s with $1$'s.
4. The resulting expansion defines $c(x)$.

• 

  Construction of $c$ in steps.

Properties

Devil's staircase is continuous
Devil's staircase is not absolutely continuous

Videos

The Devil's Staircase | Infinite Series (19 May 2017)
Devil's Staircase (19 February 2017)
Cantor's staircase (25 November 2014)

References

Cantor function