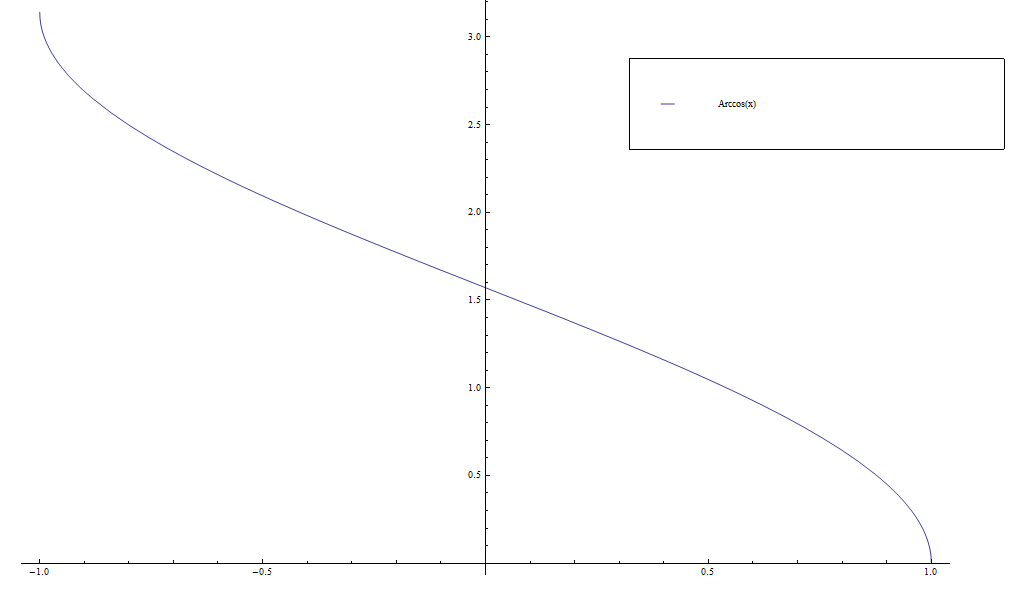
Arccos
The function $\mathrm{arccos} \colon [-1,1] \longrightarrow [0,\pi]$ is the inverse function of the cosine function.
Graph of $\mathrm{arccos}$ on $[-1,1]$.
Properties
Proposition: $$\dfrac{d}{dz} \mathrm{arccos}(z) = -\dfrac{1}{\sqrt{1-z^2}}$$
Proof: If $y=\mathrm{arccos}(z)$ then $\cos(y)=z$. Now use implicit differentiation with respect to $z$ to get
$$-\sin(y)y'=1.$$
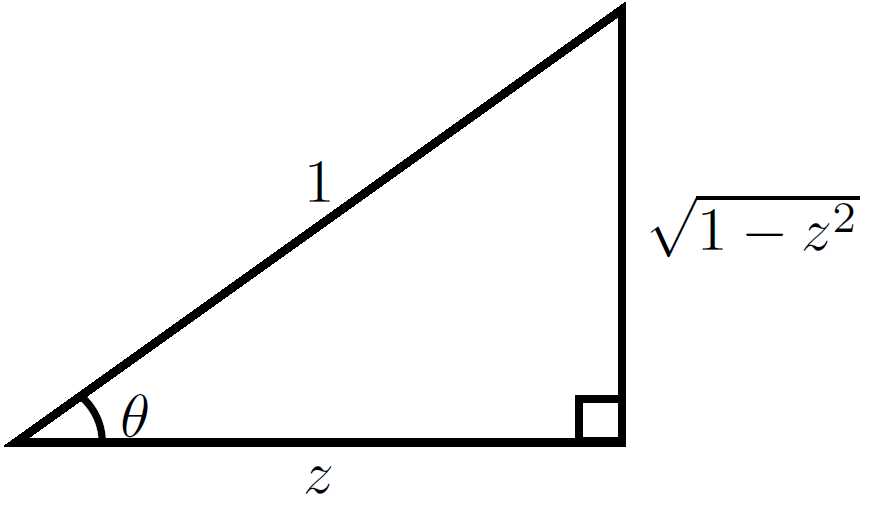
If we write $\theta=\mathrm{arccos}(z)$ then the following image shows that $\sin(\mathrm{arccos}(z))=\sqrt{1-z^2}$:
).png)
Hence substituting back in $y=\mathrm{arccos}(z)$ yields the formula
$$\dfrac{d}{dz} \mathrm{arccos}(z) = -\dfrac{1}{\sin(\mathrm{arccos}(z))} = -\dfrac{1}{\sqrt{1-z^2}}.█$$
Proposition: $$\int \mathrm{arccos}(z) dz = z\mathrm{arccos}(z)-\sqrt{1-z^2}+C$$
Proof: █
Proposition: $$\mathrm{arccos}(z)=\mathrm{arcsec} \left( \dfrac{1}{z} \right)$$
Proof: █
