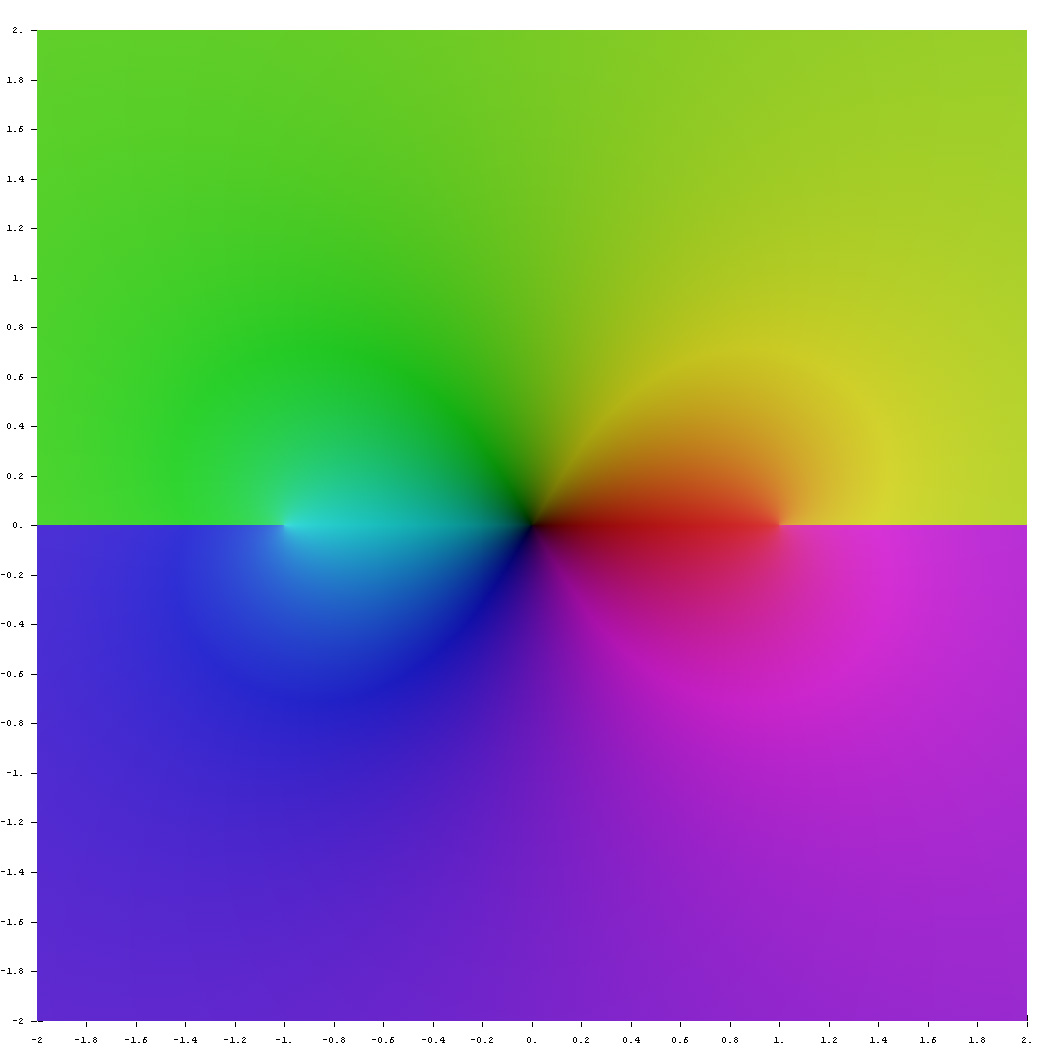
Arctanh
From specialfunctionswiki
Domain coloring of analytic continuation of $\mathrm{arctanh}$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} \chi_2(z) = \dfrac{\mathrm{arctanh}(z)}{z},$$ where $\chi$ denotes the Legendre chi function and $\mathrm{arctanh}$ denotes the inverse hyperbolic tangent function.