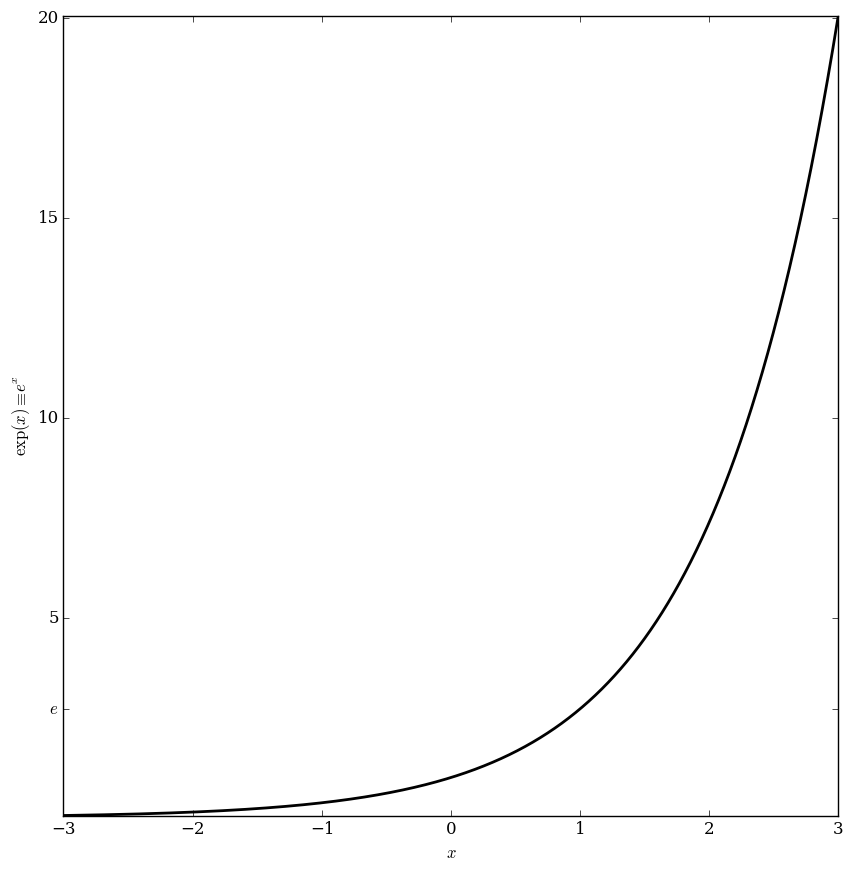
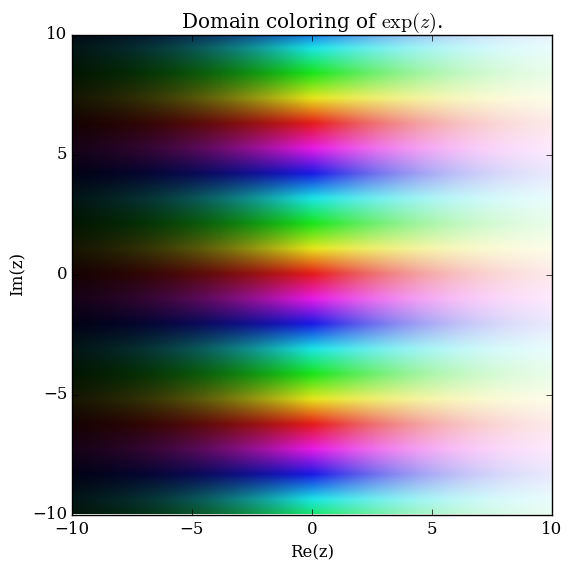
Exponential
The exponential function $\exp \colon \mathbb{C} \rightarrow \mathbb{C}$ is defined by the formula $$\exp(z) = e^z = \sum_{k=0}^{\infty} \dfrac{z^k}{k!},$$ where $e$ is the base of the natural logarithm.
Domain coloring of $\exp$.
Contents
Properties
Theorem
The following formula holds: $$\dfrac{\mathrm{d}}{\mathrm{d}z} e^z = e^z,$$ where $e^z$ denotes the exponential function.
Proof
By definition, $$e^z = \displaystyle\sum_{k=0}^{\infty} \dfrac{z^k}{k!}.$$ Term-by-term differentiation of this sum shows $$\begin{array}{ll} \dfrac{\mathrm{d}}{\mathrm{d}z} e^z &= \displaystyle\sum_{k=0}^{\infty} \dfrac{\mathrm{d}}{\mathrm{d}z} \left[ \dfrac{z^k}{k!} \right] \\ &=\displaystyle\sum_{k=1}^{\infty} \dfrac{z^{k-1}}{(k-1)!} \\ &=\displaystyle\sum_{k=0}^{\infty} \dfrac{z^k}{k!} \\ &=e^z, \end{array}$$ as was to be shown. █
References
- 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): 4.2.5
Theorem
The following formula holds: $$e^z={}_0F_0(;;z),$$ where ${}_0F_0$ denotes the hypergeometric 0F0 and $e^z$ denotes the exponential.
Proof
References
Theorem
The following formula holds for $|z|<\pi$: $$\dfrac{2e^{xt}}{e^t+1} = \sum_{k=0}^{\infty} \dfrac{E_n(x)t^n}{n!},$$ where $e^{xt}$ denotes the exponential function and $E_n$ denotes an Euler E polynomial.
Proof
References
- 1953: Arthur Erdélyi, Wilhelm Magnus, Fritz Oberhettinger and Francesco G. Tricomi: Higher Transcendental Functions Volume I ... (previous) ... (next): $\S 1.14 (2)$