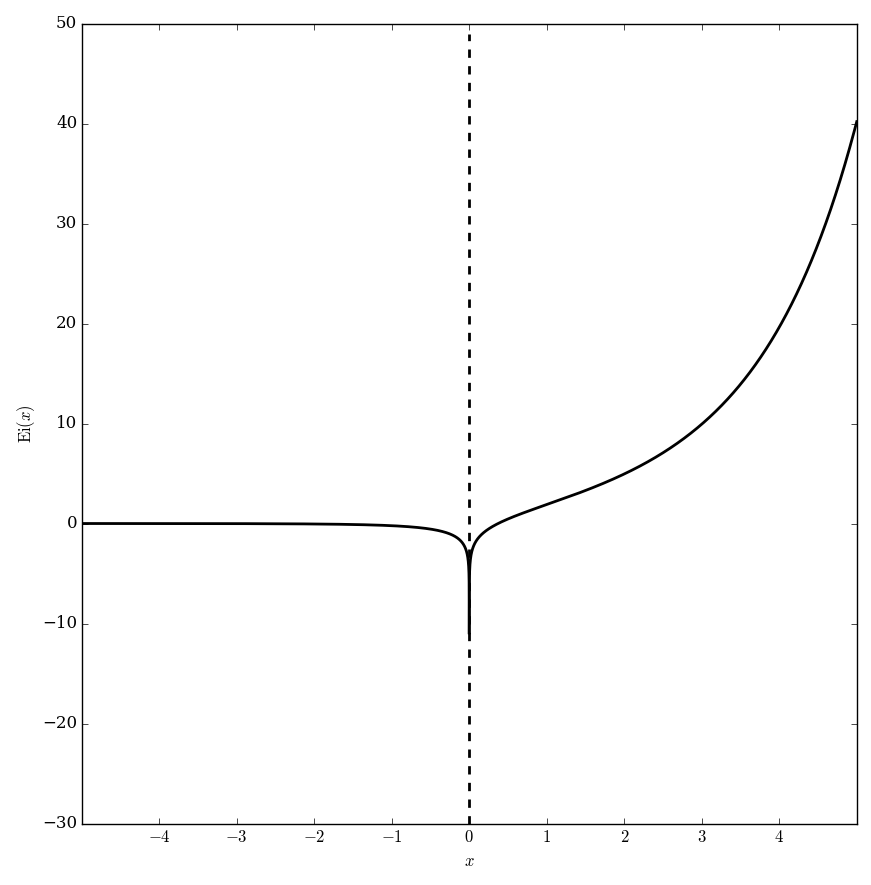
The exponential integral $\mathrm{Ei}$ is defined by $$\mathrm{Ei}(z) = \int_{-\infty}^x \dfrac{e^t}{t} \mathrm{d}t, \quad \left|\mathrm{arg}(-z) \right|<\pi.$$

Graph of $\mathrm{Ei}$.
Domain coloring of $\mathrm{Ei}$.

Properties

Theorem

The following formula holds: $$\mathrm{li}(x)=\mathrm{Ei}( \log(x)),$$ where $\mathrm{li}$ denotes the logarithmic integral, $\mathrm{Ei}$ denotes the exponential integral Ei, and $\log$ denotes the logarithm.

Proof

References

James Whitbread Lee Glaisher: On certain definite integrals involving the exponential-integral (1881)... (previous)... (next) (note: expresses this relationship as $\mathrm{Ei}(x)=\mathrm{li}(e^x)$)

Theorem

The following formula holds for $x>0$: $$\mathrm{Ei}(x) = \gamma + \log x + \displaystyle\sum_{k=1}^{\infty} \dfrac{x^k}{kk!},$$ where $\mathrm{Ei}$ denotes the exponential integral Ei, $\log$ denotes the logarithm, and $\gamma$ denotes the Euler-Mascheroni constant.

Proof

References

James Whitbread Lee Glaisher: On certain definite integrals involving the exponential-integral (1881)... (previous)... (next) (note: expresses the logarithm term as $\frac{1}{4}\log(x^4)$)

Theorem

The following formula holds: $$\mathrm{Ei}(ix)=\mathrm{Ci}(x)+i\mathrm{Si}(x),$$ where $\mathrm{Ei}$ denotes the exponential integral Ei, $\mathrm{Ci}$ denotes the cosine integral, and $\mathrm{Si}$ denotes the sine integral.