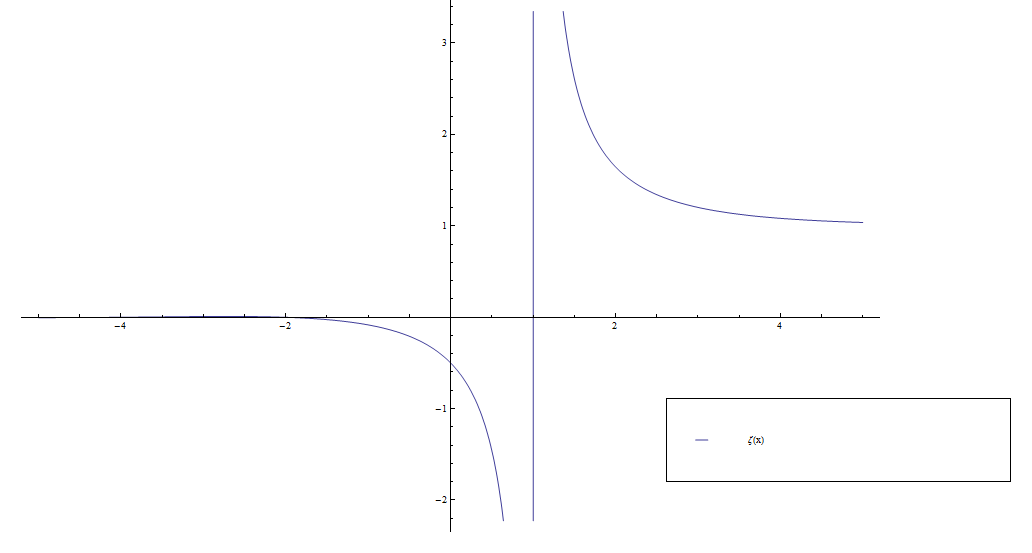
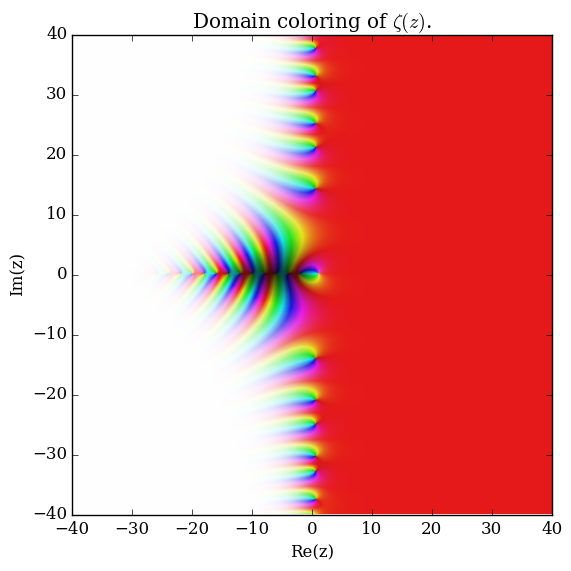
Riemann zeta

Consider the function $\zeta$ defined by the series $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z}.$$

• 

  Graph of $\zeta$ on $[-5,5]$.

• 

  Domain coloring of $\zeta$.

Properties

Proposition: If $\mathrm{Re} \hspace{2pt} z > 1$, then the series defining $\zeta(z)$ converges.

Proof: █

Theorem

The following formula holds for $\mathrm{Re}(z)>1$: $$\zeta(z)=\displaystyle\prod_{p \mathrm{\hspace{2pt} prime}} \dfrac{1}{1-p^{-z}},$$ where $\zeta$ denotes Riemann zeta.

References

• 1930: Edward Charles Titchmarsh: The Zeta-Function of Riemann ... (previous) ... (next): § Introduction $(2)$
• 1953: Harry Bateman: Higher Transcendental Functions Volume III ... (previous) ... (next): pg. $170$
• 1964: Milton Abramowitz and Irene A. Stegun: Handbook of mathematical functions ... (previous) ... (next): $23.2.2$

Theorem

The following Laurent series holds: $$\zeta(z)=\dfrac{1}{z-1} + \displaystyle\sum_{k=0}^{\infty} \dfrac{(-1)^k \lambda_k (z-1)^k}{k!},$$ where $\zeta$ denotes the Riemann zeta function and $\lambda_k$ denotes the Stieltjes constants.

References

Proposition: Let $n$ be a positive integer. Then $$\zeta(2n)=(-1)^{n+1}\dfrac{B_{2n}(2\pi)^{2n}}{2(2n)!},$$ where $B_n$ denotes the Bernoulli numbers.

Proof: █

Theorem

The following formula holds: $$P(z)=\displaystyle\sum_{k=1}^{\infty} \dfrac{\mu(k)}{k} \log \zeta(kz),$$ where $P$ denotes the Prime zeta function, $\mu$ denotes the Möbius function, $\log$ denotes the logarithm, and $\zeta$ denotes the Riemann zeta function.

Videos

Riemann Zeta function playlist

External links

• 15 Videos about the Riemann $\zeta$ function
• English translation of Riemann's paper "On the number of prime numbers less than a given quantity"
• Evaluating $\zeta(2)$
• The Riemann Hypothesis: How to make $1 Million Without Getting Out of Bed
• The Riemann Hypothesis: FAQ and resources
• How Euler discovered the zeta function
• Andrew Odlyzko: Tables of zeros of the Riemann zeta function