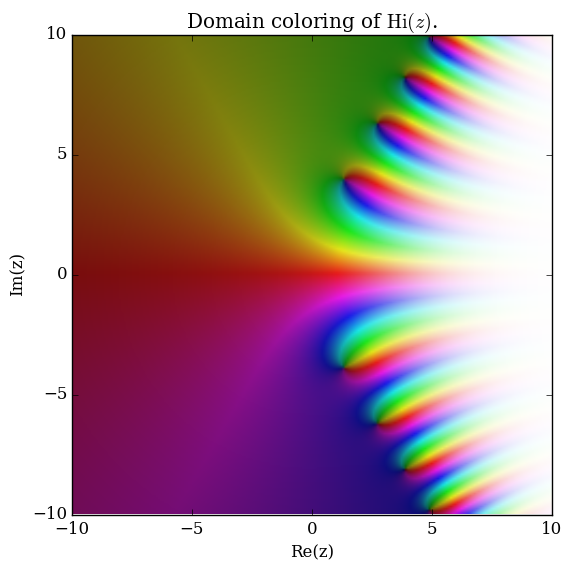
Scorer Hi

The Scorer $\mathrm{Hi}$ function is a solution of the differential equation $y(x)-x y(x)=\dfrac{1}{\pi}$ and may be defined by the formula $$\mathrm{Hi}(x)=\dfrac{1}{\pi} \displaystyle\int_0^{\infty} \exp \left( -\dfrac{t^3}{3}+xt \right)\mathrm{d}t.$$

• 

  Domain coloring of $\mathrm{Hi}$.

Properties

Relationship between Scorer Hi and Airy functions

See Also

Airy Ai
Airy Bi
Scorer Gi