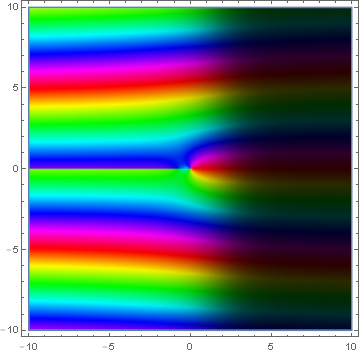
Modified Bessel K
From specialfunctionswiki
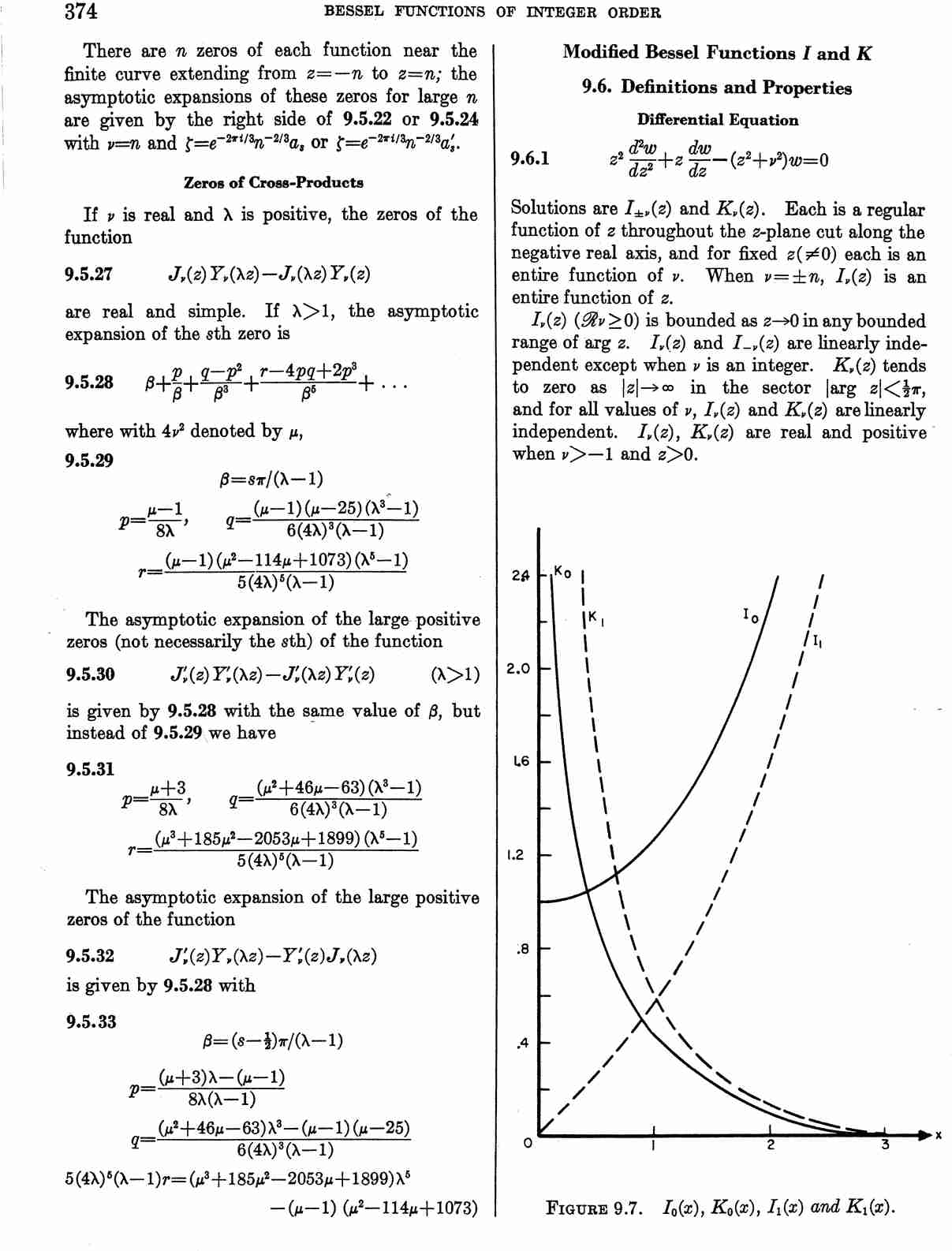
The modified Bessel function of the second kind is defined by $$K_{\nu}(z)=\dfrac{\pi}{2} \dfrac{I_{-\nu}(z)-I_{\nu}(z)}{\sin(\nu \pi)},$$ where $I_{\nu}$ is the modified Bessel function of the first kind.
Domain coloring of $K_1(z)$.
Properties
Proposition: The following formula holds: $$K_{\frac{1}{2}}(z)=\sqrt{\dfrac{\pi}{2}}\dfrac{e^{-z}}{\sqrt{z}}; z>0.$$
Proof: █
Relationship between Airy Ai and modified Bessel K
Modified Bessel $K_{\nu}$