Riemann zeta

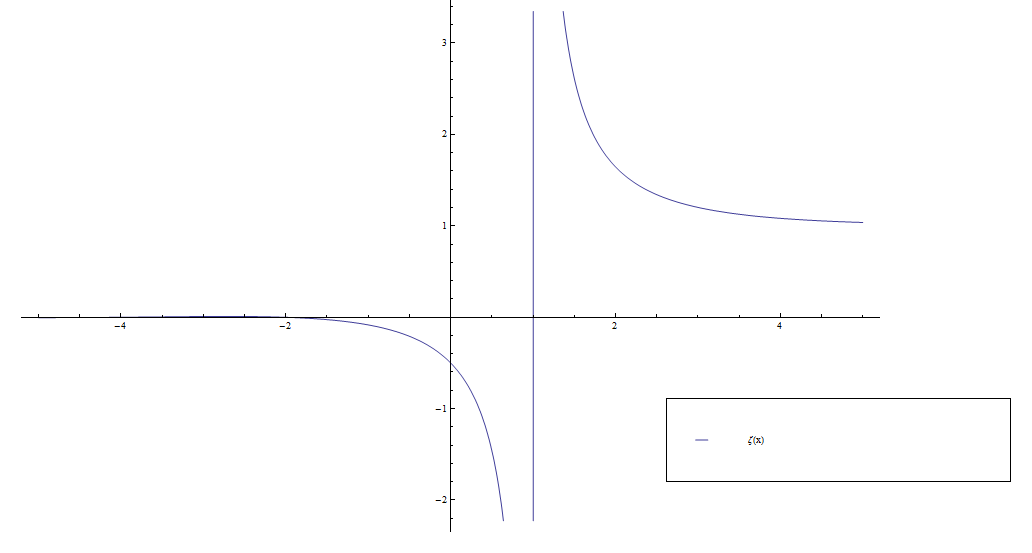
Consider the function $\zeta$ defined by the series $$\zeta(z) = \displaystyle\sum_{n=1}^{\infty} \dfrac{1}{n^z},$$ which is valid for $\mathrm{Re}(z)>1$.

• 

  Graph of $\zeta$ on $[-5,5]$.

• 

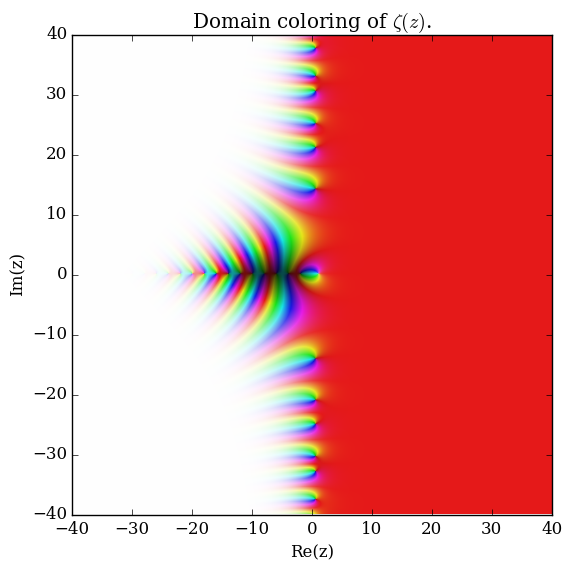
  Domain coloring of $\zeta$.

Properties

Euler product for Riemann zeta
Laurent series of the Riemann zeta function
Relationship between prime zeta, Möbius function, logarithm, and Riemann zeta

Videos

Riemann Zeta function playlist

External links

• 15 Videos about the Riemann $\zeta$ function
• English translation of Riemann's paper "On the number of prime numbers less than a given quantity"
• Evaluating $\zeta(2)$
• The Riemann Hypothesis: How to make $1 Million Without Getting Out of Bed
• The Riemann Hypothesis: FAQ and resources
• How Euler discovered the zeta function
• Andrew Odlyzko: Tables of zeros of the Riemann zeta function

References

• 1930: Edward Charles Titchmarsh: The Zeta-Function of Riemann ... (next): § Introduction (1)